题目内容
12.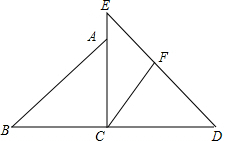 将一副三角尺拼成如图所示,∠BAC=45°,∠D=30°,∠BCA=∠DCE=90°,过点C作CF∥AB,交DE于点F,则∠EFC=75度.
将一副三角尺拼成如图所示,∠BAC=45°,∠D=30°,∠BCA=∠DCE=90°,过点C作CF∥AB,交DE于点F,则∠EFC=75度.
分析 先根据平行线的性质,即可得到∠FCD的度数,再根据三角形外角性质,即可得到∠EFC的度数.
解答 解:∵∠BCD=∠DCE=90°,
∴B,C,D在同一直线上,
∵CF∥AB,∠B=45°,
∴∠DCF=45°,
∵∠D=30°,
∴∠EFC=∠D+∠FCD=30°+45°=75°,
故答案为:75.
点评 本题主要考查了平行线的性质以及三角形外角性质的运用,解题时注意:两直线平行,同位角相等.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
3.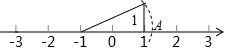 如图,在数轴上点A表示的数为a,则a的值为( )
如图,在数轴上点A表示的数为a,则a的值为( )
 如图,在数轴上点A表示的数为a,则a的值为( )
如图,在数轴上点A表示的数为a,则a的值为( )| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | 1-$\sqrt{5}$ | D. | -1+$\sqrt{5}$ |
7.下列图案中,是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.下列命题是真命题的是( )
| A. | 同位角相等 | |
| B. | 有且只有一条直线与已知直线垂直 | |
| C. | 垂线段最短 | |
| D. | 直线外一点到这条直线的垂线段,叫做点到直线的距离 |
 如图,点B在AD的延长线上,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDB=110°.
如图,点B在AD的延长线上,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDB=110°.