题目内容
15.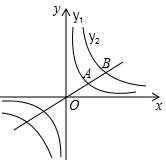 如图,过原点O的直线与反比例函数y1、y2的图象在第一象限内分别交于点A、B,且A为OB的中点.若点B的坐标为(8,2),则y1与x的函数表达式是y1=$\frac{4}{x}$.
如图,过原点O的直线与反比例函数y1、y2的图象在第一象限内分别交于点A、B,且A为OB的中点.若点B的坐标为(8,2),则y1与x的函数表达式是y1=$\frac{4}{x}$.
分析 过A作AC⊥x轴于C,过B作BD⊥x轴于D,由于点B的坐标为(8,2),即可求得A(4,1),代入反比例函数的解析式即可求出结果.
解答  解:过A作AC⊥x轴于C,过B作BD⊥x轴于D,
解:过A作AC⊥x轴于C,过B作BD⊥x轴于D,
∴AC∥BD,
∴△OAC∽△OBD,
∴$\frac{AC}{BD}$=$\frac{OC}{OD}$=$\frac{OA}{OB}$,
∵A为OB的中点,点B的坐标为(8,2),
∴$\frac{AC}{BD}$=$\frac{OC}{OD}$=$\frac{1}{2}$,
∴AC=1,OC=4,
∴A(1,4),
设y1=$\frac{k}{x}$,
∴k=1×4=4,
∴y1与x的函数表达式是y1=$\frac{4}{x}$,
故答案为y1=$\frac{4}{x}$.
点评 本题主要考查了待定系数法求反比例函数,相似三角形的判定和性质,反比例函数y=$\frac{k}{x}$中k的几何意义要注意数形结合思想的运用.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
7. 如图,已知AB∥DE,CD=CE,∠B=110°,那么∠BCD等于( )
如图,已知AB∥DE,CD=CE,∠B=110°,那么∠BCD等于( )
 如图,已知AB∥DE,CD=CE,∠B=110°,那么∠BCD等于( )
如图,已知AB∥DE,CD=CE,∠B=110°,那么∠BCD等于( )| A. | 75° | B. | 85° | C. | 140° | D. | 145° |
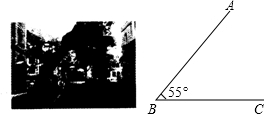 如图,小区内斜向马路的大树与地面的夹角∠ABC为55°,高为3.2米的大型客车靠近此树的一侧至少要离此树的根部B点多少米才能安全通过?(结果精确到0.1米)
如图,小区内斜向马路的大树与地面的夹角∠ABC为55°,高为3.2米的大型客车靠近此树的一侧至少要离此树的根部B点多少米才能安全通过?(结果精确到0.1米)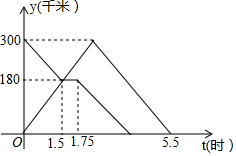 甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地,乙车匀速前往A地,中途与甲车相遇后休息了一会儿,然后以原来的速度继续行驶直到A地.设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时).y与x之间的函数图象如图所示,则乙车到达A地时甲车距B地的路程为150千米.
甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地,乙车匀速前往A地,中途与甲车相遇后休息了一会儿,然后以原来的速度继续行驶直到A地.设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时).y与x之间的函数图象如图所示,则乙车到达A地时甲车距B地的路程为150千米. 如图,四边形ABCD是⊙O的内接四边形,∠B=148°24′,则∠AOC的角度为63°12′.
如图,四边形ABCD是⊙O的内接四边形,∠B=148°24′,则∠AOC的角度为63°12′. 如图,已知直线l及点A、B,求作⊙O,使得⊙O经过点A、B,且圆心O在直线l上(尺规作图,不写作法,保留作图痕迹).
如图,已知直线l及点A、B,求作⊙O,使得⊙O经过点A、B,且圆心O在直线l上(尺规作图,不写作法,保留作图痕迹). 如图,△ABC中,∠A=46°,∠C=74°,BD平分∠ABC,交AC于点D,那么∠BDC的度数是76°.
如图,△ABC中,∠A=46°,∠C=74°,BD平分∠ABC,交AC于点D,那么∠BDC的度数是76°.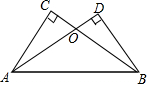 如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.
如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.