题目内容
5.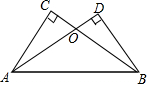 如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.
如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.(1)求证:△ACB≌△BDA.
(2)若∠ABC=35°,求∠CAO的度数.
分析 (2)由HL证明Rt△ACB≌Rt△BDA即可;
(2)由全等三角形的性质求出∠BAD=35°,由直角三角形的性质求出∠BAC=55°,即可得出所求.
解答 (1)证明:∵∠C=∠D=90°.
∴△ACB和△BDA是直角三角形,
在Rt△ACB和Rt△BDA中,$\left\{\begin{array}{l}{AB=BA}\\{BC=AD}\end{array}\right.$,
∴Rt△ACB≌Rt△BDA(HL);
(2)解:∵△ACB≌△BDA,
∴∠BAD=∠ABC=35°,
∵∠BAC=90°-∠ABC=55°,
∴∠CAO=∠BAC-∠BAD=20°.
点评 此题主要考查了全等三角形的判定与性质等知识,根据已知得出△ABC≌△BAD是解题关键.

练习册系列答案
相关题目
16.π是$\frac{1}{π}$的( )
| A. | 绝对值 | B. | 倒数 | C. | 相反数 | D. | 平方根 |
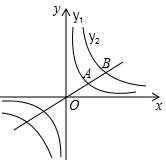 如图,过原点O的直线与反比例函数y1、y2的图象在第一象限内分别交于点A、B,且A为OB的中点.若点B的坐标为(8,2),则y1与x的函数表达式是y1=$\frac{4}{x}$.
如图,过原点O的直线与反比例函数y1、y2的图象在第一象限内分别交于点A、B,且A为OB的中点.若点B的坐标为(8,2),则y1与x的函数表达式是y1=$\frac{4}{x}$.
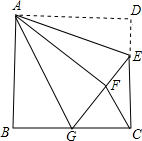 如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是①②③④⑤.
如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是①②③④⑤.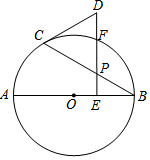 如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.
如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.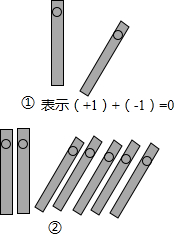 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为-3.
中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为-3.