题目内容
8.△ABC中,∠C=60°,∠A、∠B的平分线交于O,则∠AOB=120°.分析 根据三角形的内角和定理求出∠ABC+∠BAC,再根据角平分线的定义求出∠OAB+∠OBA,然后利用三角形的内角和定理列式计算即可得解.
解答 解:∵∠C=60°,
∴∠ABC+∠BAC=180°-60°=120°,
∵∠CAB与∠CBA的平分线相交于O点,
∴∠OAB+∠OBA=$\frac{1}{2}$(∠ABC+∠BAC)=$\frac{1}{2}$×120°=60°,
在△AOB中,∠AOB=180°-(∠OAB+∠OBA)=180°-60°=120°.
故答案为120°
点评 本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
相关题目
18.下列命题中的真命题是( )
| A. | 长度相等的弧是等弧 | B. | 相似三角形的面积比等于相似比 | ||
| C. | 正方形不是中心对称图形 | D. | 圆内接四边形的对角互补 |
20.下列命题是假命题的是( )
| A. | ±$\frac{1}{5}$是$\frac{1}{25}$的平方根 | B. | 81的平方根是9 | ||
| C. | 0.04的算术平方根是0.2 | D. | -27的立方根是-3 |
17.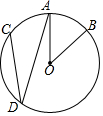 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )| A. | 15° | B. | 20° | C. | 30° | D. | 40° |
 如图,反比例函数y=$\frac{3}{x}$的图象与一次函数y=x+2的图象交于A、B两点.
如图,反比例函数y=$\frac{3}{x}$的图象与一次函数y=x+2的图象交于A、B两点.
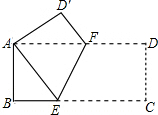 如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为4$\sqrt{5}$.
如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为4$\sqrt{5}$.