题目内容
8. 如图,若AB∥CD,AC⊥BD,AD∥BC,则图中共有全等三角形8个.
如图,若AB∥CD,AC⊥BD,AD∥BC,则图中共有全等三角形8个.
分析 根据平行四边形和菱形的判定得出四边形是菱形和平行四边形,推出AD=DC=AB=BC,AO=OC,OB=OD,再根据全等三角形的判定逐个判断即可.
解答 解:∵AB∥CD,AC⊥BD,AD∥BC,
∴四边形ABCD是平行四边形,
∴四边形ABCD是菱形,
∴AD=DC=AB=BC,AO=OC,OB=OD,
在△BAD和△DCB中
$\left\{\begin{array}{l}{AB=CD}\\{BD=DB}\\{AD=CB}\end{array}\right.$
∴△BAD≌△DCB(SSS),
同理△ADC≌△CBA,
在△ADO和△CBO中
$\left\{\begin{array}{l}{AO=OC}\\{OD=OB}\\{AD=CB}\end{array}\right.$
∴△ADO≌△CBO(SSS),
同理△ABO≌△CDO,
在△ADO和△CDO中
$\left\{\begin{array}{l}{OD=OD}\\{AO=OC}\\{AD=DC}\end{array}\right.$
∴△ADO≌△CDO(SSS),
∴△ADO≌△CDO≌△ABO≌△CBO,
即共有2+6=8对全等三角形,
故答案为:8.
点评 本题考查了全等三角形的判定定理,平行四边形的性质和判定,菱形的性质和判定的应用,能综合运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
 如图,正方形ABCD和正方形CEFG有公共顶点C,点C的坐标是C(6,4),点B,E,F在x轴上,点A在y轴上,反比例函数y=$\frac{k}{x}$的图象经过CE的中点Q.
如图,正方形ABCD和正方形CEFG有公共顶点C,点C的坐标是C(6,4),点B,E,F在x轴上,点A在y轴上,反比例函数y=$\frac{k}{x}$的图象经过CE的中点Q.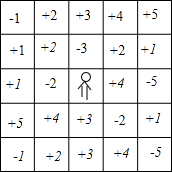 如图是一个“冲出围城”的游戏,规则是:城中人想要冲出围城,可以横走也可以竖走,但不可以斜走,每走一格就可以得到格中相应的分数作为生命值,每格中的分数用乘法累计.当生命值小于+9,并且处于最外圈时,就可以冲出围城,生命值为负数不可以出城.例如:(-2)×(+2)×(+2)×(-1)=+8,就是一条冲出围城的路线.把你找到的冲出围城的路线写下来,也可以直接用箭头将路线在表中表示出来.
如图是一个“冲出围城”的游戏,规则是:城中人想要冲出围城,可以横走也可以竖走,但不可以斜走,每走一格就可以得到格中相应的分数作为生命值,每格中的分数用乘法累计.当生命值小于+9,并且处于最外圈时,就可以冲出围城,生命值为负数不可以出城.例如:(-2)×(+2)×(+2)×(-1)=+8,就是一条冲出围城的路线.把你找到的冲出围城的路线写下来,也可以直接用箭头将路线在表中表示出来.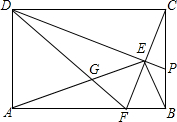 如图所示,在矩形ABCD中.AB=4,BC=3.点F、P分别为线段AB、BC上的动点,CF与DP交于点E,DF与AE交于点G.若GF•DG=AG•GE,连结BE,则BE的最小值为$\sqrt{13}$-2.
如图所示,在矩形ABCD中.AB=4,BC=3.点F、P分别为线段AB、BC上的动点,CF与DP交于点E,DF与AE交于点G.若GF•DG=AG•GE,连结BE,则BE的最小值为$\sqrt{13}$-2.