题目内容
20.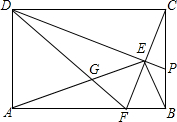 如图所示,在矩形ABCD中.AB=4,BC=3.点F、P分别为线段AB、BC上的动点,CF与DP交于点E,DF与AE交于点G.若GF•DG=AG•GE,连结BE,则BE的最小值为$\sqrt{13}$-2.
如图所示,在矩形ABCD中.AB=4,BC=3.点F、P分别为线段AB、BC上的动点,CF与DP交于点E,DF与AE交于点G.若GF•DG=AG•GE,连结BE,则BE的最小值为$\sqrt{13}$-2.
分析 取CD的中点O连接OE,OB,由GF•DG=AG•GE,于是得到比例式$\frac{GF}{GE}=\frac{AG}{DG}$,$\frac{GF}{AG}=\frac{GE}{DG}$,证得△AGF∽△DGE,△EFG∽△DAG,由相似三角形的性质得到∠DEG=∠AFG,∠GEF=∠DAG,求得∠CED=90°,根据直角三角形的性质得到OE=$\frac{1}{2}$CD=2,根据勾股定理得到OB=$\sqrt{O{C}^{2}+B{C}^{2}}$=$\sqrt{13}$,根据圆周角定理得到∠CED=90°,得到点E在以CD为直径的⊙O上运动,于是得到结论.
解答  解:取CD的中点O连接OE,OB,
解:取CD的中点O连接OE,OB,
∵GF•DG=AG•GE,
∴$\frac{GF}{GE}=\frac{AG}{DG}$,$\frac{GF}{AG}=\frac{GE}{DG}$,
∴△AGF∽△DGE,△EFG∽△DAG,
∴∠DEG=∠AFG,∠GEF=∠DAG,
∴∠DEF=∠DEG+∠GEF=∠AFG+∠GDA=90°,
∴∠CED=90°,
∴OE=$\frac{1}{2}$CD=2,
∵OB=$\sqrt{O{C}^{2}+B{C}^{2}}$=$\sqrt{13}$,
∵∠CED=90°,
∴点E在以CD为直径的⊙O上运动,
∴BE≥OB-OE,当点E在OB上时,BE=OB-OE=$\sqrt{13}$-2,
∴BE的最小值为$\sqrt{13}$-2,
故答案为:$\sqrt{13}$-2.
点评 本题考查了相似三角形的判定和性质,矩形的性质,勾股定理,圆周角定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
9.其中,从左面看到的形状图是平行四边形的有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
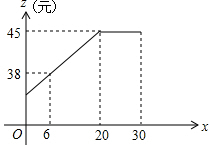 大学生李某毕业响应国家“自主创业”的号召,在我市沙坪坝学校密集的沙南街路段投资开办了一个学生文具店.该店在开学前8月31日购进一种今年新上市的文具袋9月份(9月1日至9月30日)进行30天的试销售,购进价格为20元/个.销售结束后得知日销售量y(个)与销售时间x(天)之间有如下关系:y=-2x+80(1≤x≤30,x取正整数);又知销售价格z(元/个)与销售时间x(天,x取正整数)之间的函数关系满足如图所示的函数图象.
大学生李某毕业响应国家“自主创业”的号召,在我市沙坪坝学校密集的沙南街路段投资开办了一个学生文具店.该店在开学前8月31日购进一种今年新上市的文具袋9月份(9月1日至9月30日)进行30天的试销售,购进价格为20元/个.销售结束后得知日销售量y(个)与销售时间x(天)之间有如下关系:y=-2x+80(1≤x≤30,x取正整数);又知销售价格z(元/个)与销售时间x(天,x取正整数)之间的函数关系满足如图所示的函数图象. 如图,若AB∥CD,AC⊥BD,AD∥BC,则图中共有全等三角形8个.
如图,若AB∥CD,AC⊥BD,AD∥BC,则图中共有全等三角形8个. 把一张矩形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=8cm,BC=16cm.
把一张矩形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=8cm,BC=16cm.