题目内容
19.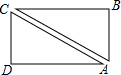 传说中愚公移山后,为了陶冶性情,在自家门前开了一个长方形人工湖,如图,愚公每次出门赶集,都要从家中A点出发,经过B或D点到集市C点,久而久之,他发观这样太浪费时间.于是决定在A,C之间修一条水上长廊,已知AD=8000米,CD=6000米,步行速度为4千米/时.问:长廊修好后,愚公每次去集市可节省多少时间?
传说中愚公移山后,为了陶冶性情,在自家门前开了一个长方形人工湖,如图,愚公每次出门赶集,都要从家中A点出发,经过B或D点到集市C点,久而久之,他发观这样太浪费时间.于是决定在A,C之间修一条水上长廊,已知AD=8000米,CD=6000米,步行速度为4千米/时.问:长廊修好后,愚公每次去集市可节省多少时间?
分析 首先根据勾股定理求得对角线AC的长,然后求得AD+DC的和,二者相减即可求得少走的路程,除以速度即可求得时间.
解答 解:∵AD⊥DC,AD=8000米,CD=6000米,
∴AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{800{0}^{2}+600{0}^{2}}$=10000米,
∵AD+DC=6000+8000=14000米,
∴走人工水上长廊比绕道D点少走14000-10000=4000米,
∵步行速度为4千米/时,
∴共节约1小时.
点评 本题考查了勾股定理的应用,解题的关键是能够从实际问题中抽象出直角三角形,难度不大.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
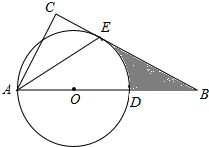 如图,在△ABC中,AE是它的角平分线,∠C=90°,∠B=30°,D在AB边上,AD=4,以AD为直径的圆O经过点E.
如图,在△ABC中,AE是它的角平分线,∠C=90°,∠B=30°,D在AB边上,AD=4,以AD为直径的圆O经过点E.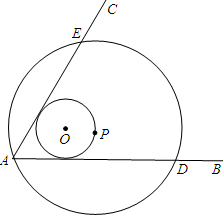 如图,∠BAC=60°,半径长为1的圆O与∠BAC的两边相切,P为圆O上一动点,以P为圆心,PA长为半径的圆P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为3$\sqrt{3}$.
如图,∠BAC=60°,半径长为1的圆O与∠BAC的两边相切,P为圆O上一动点,以P为圆心,PA长为半径的圆P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为3$\sqrt{3}$.