题目内容
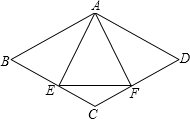 (1)已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且CE=CF.求证:AE=AF.
(1)已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且CE=CF.求证:AE=AF.(2)根据省政府要求,我市2012年要完成“三沿一环”补植、造林更新、城镇绿化总面积39.5万亩.其中:“三沿一环”(沿路、沿江、沿海、环城)补植15万亩;造林更新面积比城镇绿化面积的3倍还多2.5万亩.请你根据以上提供的信息,求造林更新和城镇绿化面积各多少万亩?
考点:菱形的性质,二元一次方程组的应用
专题:
分析:(1)首先根据菱形的性质可得AB=AD=BC=CD,∠B=∠D,然后再证明△ABE≌△ADF,可得AE=AF;
(2)首先造林更新面积为x万亩,城镇绿化面积为y万亩,根据题意可得等量关系:①“三沿一环”补植面积+造林更新面积+城镇绿化面积=39.5万亩;②造林更新面积=城镇绿化面积的3倍+2.5万亩,根据等量关系列出方程组,再解即可.
(2)首先造林更新面积为x万亩,城镇绿化面积为y万亩,根据题意可得等量关系:①“三沿一环”补植面积+造林更新面积+城镇绿化面积=39.5万亩;②造林更新面积=城镇绿化面积的3倍+2.5万亩,根据等量关系列出方程组,再解即可.
解答:(1)证明:∵四边形ABCD是菱形,
∴AB=AD=BC=CD,∠B=∠D,
∵CE=CF,
∴BC-CE=DC-CF,
即:BE=FD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(SAS),
∴AE=AF;
(2)解:设造林更新面积为x万亩,城镇绿化面积为y万亩,
依题意得:
,
解
.
答:造林更新面积为19万亩,城镇绿化面积为5.5万亩.
∴AB=AD=BC=CD,∠B=∠D,
∵CE=CF,
∴BC-CE=DC-CF,
即:BE=FD,
在△ABE和△ADF中,
|
∴△ABE≌△ADF(SAS),
∴AE=AF;
(2)解:设造林更新面积为x万亩,城镇绿化面积为y万亩,
依题意得:
|
解
|
答:造林更新面积为19万亩,城镇绿化面积为5.5万亩.
点评:此题主要考查了菱形的性质,以及二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系,列出方程组.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
在△ABC中,a,b,c分别是∠A,∠B,∠C所对的边,有下列命题:
①若a2+b2≠c2,则△ABC不是直角三角形;
②若△ABC是直角三角形,∠C=90°,则a2+b2=c2;
③若a2-b2=c2,则△ABC 是直角三角形;
④若a2+c2=b2,则∠B=90°.
其中正确的有( )
①若a2+b2≠c2,则△ABC不是直角三角形;
②若△ABC是直角三角形,∠C=90°,则a2+b2=c2;
③若a2-b2=c2,则△ABC 是直角三角形;
④若a2+c2=b2,则∠B=90°.
其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列判断错误的是( )
| A、多项式5x2-2x+4是二次三项式 | ||
| B、单项式-a2b3c4的系数是-1,次数是9 | ||
C、式子m+5,ab,x=1,-2,
| ||
| D、当k=3时,关于x,y的代数式(-3kxy+3y)+(9xy-8x+1)中不含二次项 |
下列命题中,假命题是( )
| A、梯形的两条对角线相等 |
| B、矩形的两条对角线相等 |
| C、菱形的两条对角线互相垂直 |
| D、正方形的每一条对角线平分一组对角 |
下列图形中,不一定是轴对称图形的是( )
| A、等边三角形ABC |
| B、直角三角形ABC |
| C、线段MN |
| D、锐角∠AOB |
 如图,图象l1反映了某公司产品的销售收入y(单位:元)与销售量x(单位:吨)之间的关系,图象l2反映了该公司产品的产品成本y(元)与销售量x(吨)之间的关系,请根据图中所提供的信息解答下列问题:
如图,图象l1反映了某公司产品的销售收入y(单位:元)与销售量x(单位:吨)之间的关系,图象l2反映了该公司产品的产品成本y(元)与销售量x(吨)之间的关系,请根据图中所提供的信息解答下列问题: 如图,已知:ABCD是正方形,E是AD的中点.
如图,已知:ABCD是正方形,E是AD的中点. 已知:△ABC中,CD⊥AB,AC2=AD•AB,求证:CD2=AD•BD.
已知:△ABC中,CD⊥AB,AC2=AD•AB,求证:CD2=AD•BD.