题目内容
已知：△ABC中，CD⊥AB，AC2=AD•AB，求证：CD2=AD•BD．考点：相似三角形的判定与性质
专题：证明题
分析：求出
=
，然后根据两边对应成比例，夹角相等两三角形相似求出△ABC和△ACD相似，根据相似三角形对应角相等可得∠B=∠ACD，根据垂直的定义可得∠ADC=∠CDB=90°，再根据两角对应相等，两三角形相似求出△ACD和△CBD相似，然后根据相似三角形对应边成比例列式整理即可得证．
| AC |
| AD |
| AB |
| AC |
解答：证明：∵AC2=AD•AB，
∴
=
，
又∵∠BAC=∠CAD，
∴△ABC∽△ACD，
∴∠B=∠ACD，
∵CD⊥AB，
∴∠ADC=∠CDB=90°，
∴△ACD∽△CBD，
∴
=
，
∴CD2=AD•BD．
∴
| AC |
| AD |
| AB |
| AC |
又∵∠BAC=∠CAD，
∴△ABC∽△ACD，
∴∠B=∠ACD，
∵CD⊥AB，
∴∠ADC=∠CDB=90°，
∴△ACD∽△CBD，
∴
| CD |
| BD |
| AD |
| CD |
∴CD2=AD•BD．
点评：本题考查了相似三角形的判定与性质，解答本题关键在于把乘积式转化为比例式．
练习册系列答案
阅读快车系列答案
相关题目
下列图形的左视图与其它明显不同的是（ ）
A、 |
B、 |
C、 |
D、 |
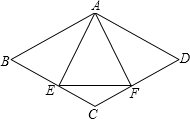（1）已知：如图，菱形ABCD中，E，F分别是CB，CD上的点，且CE=CF．求证：AE=AF．
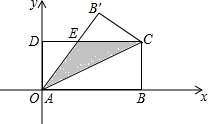如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点B落在B′处．
已知：抛物线y=ax2+bx+c与直线y=x+3分别交于x轴和y轴上同一点，交点分别是点A和点C，且抛物线的对称轴为直线x=-2．
如图，在六边形ABCDEF中，AF∥CD，∠A=140°，∠C=165°．
如图，在平行四边形ABCD中，E、F分别是对边BC和AD上的两点，且DF=BE．