题目内容
 如图,图象l1反映了某公司产品的销售收入y(单位:元)与销售量x(单位:吨)之间的关系,图象l2反映了该公司产品的产品成本y(元)与销售量x(吨)之间的关系,请根据图中所提供的信息解答下列问题:
如图,图象l1反映了某公司产品的销售收入y(单位:元)与销售量x(单位:吨)之间的关系,图象l2反映了该公司产品的产品成本y(元)与销售量x(吨)之间的关系,请根据图中所提供的信息解答下列问题:(1)当销售量为2吨时,销售收入为
(2)当销售量在什么范围内,该公司就赢利(收入大于成本)?
(3)求图中的射线l2所对应的函数关系式.
考点:一次函数的应用
专题:
分析:(1)通过图象观察当x=2时对应的与l1的交点的纵坐标是2000元,就可以得出销售收入;从图象可以看出l1与l2的交点坐标为(4,4000),就有可以求出结论;
(2)通过图象可以看出l1与l2的交点坐标为(4,4000),进一步观察图象得出答案即可;
(3)设l2的解析式为y2=k2x+b2,利用图象上的坐标就可以求出结论.
(2)通过图象可以看出l1与l2的交点坐标为(4,4000),进一步观察图象得出答案即可;
(3)设l2的解析式为y2=k2x+b2,利用图象上的坐标就可以求出结论.
解答:解:(1)通过图象观察可以得出,当x=2时,对应的与l1的交点是(2,2000),
所以当销售量为2吨时,销售收入2000元;
当x=4时,对应的l2与l1的交点是(4,2000);
(2)从图象观察可以得出:l1与l2的交点坐标是(4,4000),
则当销售量大于4吨时,该公司就赢利;
(3)设l2的解析式为y2=k2x+b2,由图象,得
,
解得:
,
故l2的解析式为:y2=500x+2000,
所以当销售量为2吨时,销售收入2000元;
当x=4时,对应的l2与l1的交点是(4,2000);
(2)从图象观察可以得出:l1与l2的交点坐标是(4,4000),
则当销售量大于4吨时,该公司就赢利;
(3)设l2的解析式为y2=k2x+b2,由图象,得
|
解得:
|
故l2的解析式为:y2=500x+2000,
点评:本题是一道一次函数的综合试题,考查了运用待定系数法求函数的解析式的运用,识别函数图象和会分析函数图象的能力及一次函数与一元一次方程的结合的运用,搞清楚交点意义和图象的相对位置是关键.

练习册系列答案
相关题目
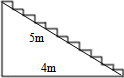 某宾馆准备在大厅的主楼道上铺设某种红色地毯,已知这种地毯售价为30元/m2,主楼道宽2m,其侧面如图,则购买地毯至少需要( )
某宾馆准备在大厅的主楼道上铺设某种红色地毯,已知这种地毯售价为30元/m2,主楼道宽2m,其侧面如图,则购买地毯至少需要( )| A、240元 | B、360元 |
| C、420元 | D、480元 |
 如图,AB是⊙O的直径,弦CD⊥AB,∠C=30°,CD=2
如图,AB是⊙O的直径,弦CD⊥AB,∠C=30°,CD=2| 3 |
| A、π | ||
| B、2π | ||
C、
| ||
| D、π |
如图,ABCD是一张平行四边形纸片,要求利用所学知识作出一个菱形,甲、乙两位同学的作法如下:则关于甲、乙两人的作法,下列判断正确的为( )


| A、仅甲正确 |
| B、仅乙正确 |
| C、甲、乙均正确 |
| D、甲、乙均错误 |
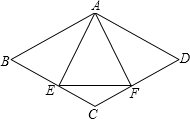 (1)已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且CE=CF.求证:AE=AF.
(1)已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且CE=CF.求证:AE=AF.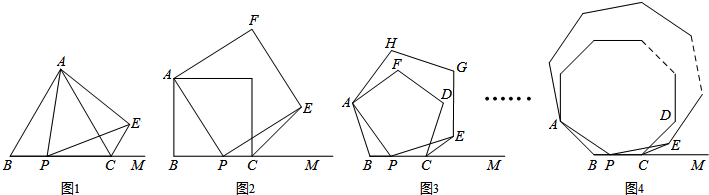
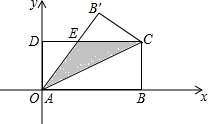 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在B′处.
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在B′处. 如图,在六边形ABCDEF中,AF∥CD,∠A=140°,∠C=165°.
如图,在六边形ABCDEF中,AF∥CD,∠A=140°,∠C=165°. 实数a、b、c在数轴上的对应点表示出来如图所示:请化简:
实数a、b、c在数轴上的对应点表示出来如图所示:请化简: