题目内容
6.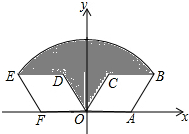 如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则线段OB=2$\sqrt{3}$;图中阴影部分的面积为4π-2$\sqrt{3}$.
如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则线段OB=2$\sqrt{3}$;图中阴影部分的面积为4π-2$\sqrt{3}$.
分析 过点B作BG⊥x轴于点G,连接OE,OB,由菱形OABC的顶点A的坐标为(2,0),可求得OA=2,又由将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,∠COA=60°,可求得∠AOB=∠EOF=30°,AB=OA=2,继而求得线段BG的长,则可求得扇形EOB与菱形OABC的面积,继而求得答案.
解答 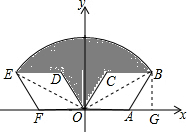 解:过点B作BG⊥x轴于点G,连接OE,OB,
解:过点B作BG⊥x轴于点G,连接OE,OB,
∵菱形OABC的顶点A的坐标为(2,0),
∴OA=2,
∵将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,∠COA=60°,
则∠AOB=∠EOF=30°,AB=OA=2,
∴∠BAG=60°,
∴∠ABG=30°,
∴AG=$\frac{1}{2}$AB=1,BG=$\sqrt{A{B}^{2}-A{G}^{2}}$=$\sqrt{3}$,
∴OB=2BG=2$\sqrt{3}$,
∵∠BOE=120°,
∴S扇形=$\frac{120π×(2\sqrt{3})^{2}}{360}$=4π,S菱形OABC=OA•BG=2$\sqrt{3}$,
∴S阴影=S扇形-S菱形OABC=4π-2$\sqrt{3}$.
故答案为:2$\sqrt{3}$,4π-2$\sqrt{3}$.
点评 此题考查了菱形的性质、旋转的性质以及扇形的面积.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
16.不等式组$\left\{\begin{array}{l}{x-2<0}\\{2x+6>0}\end{array}\right.$的解集为( )
| A. | -2<x<3 | B. | -3<x<2 | C. | x<2 | D. | x>-3 |
2.如果不等式(1+a)x>1+a的解集为x<1,那么a的取值范围是( )
| A. | a>0 | B. | a<0 | C. | a>-1 | D. | a<-1 |
11.估计$\sqrt{7}-2$的值在( )
| A. | 0到1之间 | B. | 1到2之间 | C. | 2到3之间 | D. | 3至4之间 |
15.$\sqrt{(-49)^{2}}$的平方根是( )
| A. | 49 | B. | 7 | C. | ±7 | D. | ±49 |
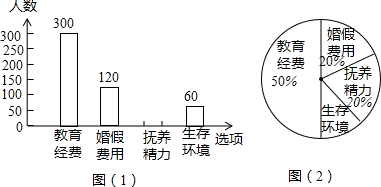
 如图,是某射击运动员在一次射击训练时10次射击后的成绩(环数)制成的条形统计图,求这10次射击后的成绩的平均数、众数和中位数.
如图,是某射击运动员在一次射击训练时10次射击后的成绩(环数)制成的条形统计图,求这10次射击后的成绩的平均数、众数和中位数.