题目内容
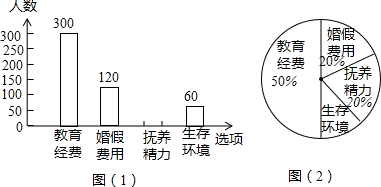
20.为适应未来人口发展的需要,国家逐步放开了生育二胎的限制,但是2015年的调查显示,只有不足四成家庭希望生育二胎.某中学九(1)班为了了解困扰适龄夫妻生育二胎意愿的原因,采取街头随机抽样调查的方法,调查了若干名适龄男女的意见,并绘制成如图所示的两幅不完整的统计图,(如图(1)、图(2),要求每个被访者只能选择一种),请你根据图中提供的信息解答下列问题:(1)本次调查的适龄男女的总数是600人.在扇形统计图中“生存环境”所在扇形的圆心角的度数是36°.
(2)请你补全条形统计图.
(3)同学们根据自己的调查结果进行了进一步的数据收集和分析,发现仅从改善学生的教育环境而言,某地区的教育经费投入是连年增加,2014年的投入已经达到了800亿元,如果2016年该地区预计在教育方面投入882亿元,那么该地区每年的教育经费投入的平均增长率应保持在多少?
分析 (1)根据样本总数=选“教育经费”人数÷其所占比例,即可得出本次调查的适龄男女的总数,由圆心角=所占比例×360°,即可得出结论;
(2)由样本总数-选其他三项的人数即可得出选“抚养精力”的人数,由此数据补充完条形统计图即可;
(3)该地区每年的教育经费投入的平均增长率为x,根据2016年费用=2014年费用×(1+增长率)的平方列出关于x的一元二次方程,解方程即可得出结论.
解答 解:(1)300÷50%=600(人);
360°×(1-50%-20%-20%)=36°.
故答案为:600;36°.
(2)600-300-120-60=120(人),
补全条形统计图如下图.
(3)该地区每年的教育经费投入的平均增长率为x,
由已知得:800×(1+x)2=882,
解得:x=0.05,或x=-2.05(舍去).
故该地区每年的教育经费投入的平均增长率应保持在5%.
点评 本题考查了一元二次方程的应用、条形统计图以及扇形统计图,解题的关键:(1)会根据统计图解决问题;(2)熟悉条形统计图的制作;(3)由数量关系列出关于x的一元二次方程.本题属于基础题,难度不大,解题的关键是根据数量关系得出关于未知数的方程(方程组或不等式)是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.-x(x-y)(x-m)+xy(x-y)(x-n)的公因式是( )
| A. | x | B. | x-y | C. | -x(x-y) | D. | (x-m)(x-n) |
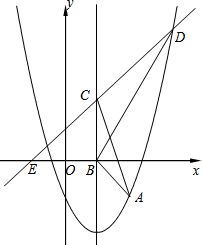 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-1经过点A(2,-1),它的对称轴与x轴相交于点B.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-1经过点A(2,-1),它的对称轴与x轴相交于点B. 如图所示的几何体是由六个小正方体组合而成的,它的左视图是( )
如图所示的几何体是由六个小正方体组合而成的,它的左视图是( )



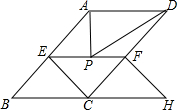 如图,在?ABCD中,AB=7,BC=5,sinB=$\frac{4}{5}$,将?ABCD折叠,使点A落在点C上,点D的对应点为H,折痕为EF.
如图,在?ABCD中,AB=7,BC=5,sinB=$\frac{4}{5}$,将?ABCD折叠,使点A落在点C上,点D的对应点为H,折痕为EF.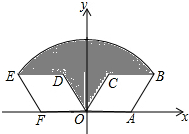 如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则线段OB=2$\sqrt{3}$;图中阴影部分的面积为4π-2$\sqrt{3}$.
如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则线段OB=2$\sqrt{3}$;图中阴影部分的面积为4π-2$\sqrt{3}$.