题目内容
16.某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调整,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:(Ⅰ)本次接受随机抽样调查的学生人数为40,图①中m的值为25.
(Ⅱ)求本次调查获取的样本数据的众数、中位数和平均数.
(Ⅲ)根据样本数据,估计该校一周的课外阅读时间大于6h的学生人数.

分析 (1)根据阅读时间为4h的人数及所占百分比可得,将时间为6小时人数除以总人数可得;
(2)根据众数、中位数、加权平均数的定义计算可得;
(3)将样本中课外阅读时间大于6h的学生人数所占比例乘以总人数1200可得.
解答 解:(1)本次接受随机抽样调查的学生人数为:$\frac{6}{0.15}=40$(人),图①中m的值为$\frac{10}{40}$×100=25;
(2)∵这组样本数据中,5出现了12次,出现次数最多,
∴这组数据的众数为5;
∵将这组数据从小到大排列,其中处于中间的两个数均为6,有$\frac{6+6}{2}$=6,
∴这组数据的中位数是6;
由条形统计图可得$\overline{x}$=$\frac{4×6+5×12+6×10+7×8+8×4}{40}$=5.8,
∴这组数据的平均数是5.8.
(3)$\frac{8+4}{40}×1200$=360(人).
答:估计该校一周的课外阅读时间大于6h的学生人数约为360人.
故答案为:(1)40,25.
点评 本题考查的是扇形统计图与条形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.

练习册系列答案
相关题目
6.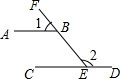 如图,已知AB∥CD,∠2=140°,则∠1=( )
如图,已知AB∥CD,∠2=140°,则∠1=( )
 如图,已知AB∥CD,∠2=140°,则∠1=( )
如图,已知AB∥CD,∠2=140°,则∠1=( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. | 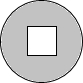 |
11.将5个相同的球放入位于一排的8个格子中,每格至多放一个球,则3个空格相连的概率是( )
| A. | $\frac{3}{28}$ | B. | $\frac{5}{28}$ | C. | $\frac{3}{56}$ | D. | $\frac{5}{56}$ |
5.在某校举行的“汉字听写”大赛中,七名学生听写汉字的个数分别为350,310,320,250,310,340,360,则这组数据的中位数是( )
| A. | 330 | B. | 320 | C. | 310 | D. | 250 |
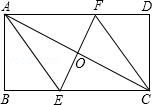 如图,将矩形ABCD折叠,使点A与点C重合,折痕交BC、AD分别于点E、F.
如图,将矩形ABCD折叠,使点A与点C重合,折痕交BC、AD分别于点E、F.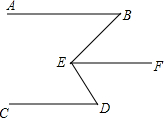 如图,已知∠B=∠BEF,EF∥CD,试判断AB与CD是否平行?
如图,已知∠B=∠BEF,EF∥CD,试判断AB与CD是否平行?