题目内容
2．m为什么实数时，方程$\frac{5m}{2}$-$\frac{x}{4}$=$\frac{3}{2}$的解在2与4之间？分析 先解一元一次方程得到x=10m-6，则根据题意得到不等式组2＜10m-6＜4，然后根据不等式的性质解不等式组．
解答 解：去分母得10m-x=6，
则x=10m-6，
所以2＜10m-6＜4，
则8＜10m＜10，
所以$\frac{4}{5}$＜m＜1．
点评 本题考查了解一元一次不等式组：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．也考查了解一元一次方程的解．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
如图所示，点A的坐标为（2，1），点B的坐标为（5，3），点C为x轴上一动点，则AC+BC的最小值为5．
10．关于x的不等式组$\left\{\begin{array}{l}{x-1＞0}\\{{x}^{3}-{x}^{2}+x≤k}\end{array}\right.$的正整数解只有2和3，则|k-21|+|k-52|+1975的值为（ ）
| A． | 2004 | B． | 2005 | C． | 2006 | D． | 2007 |
如图所示，AB=DC，AD=BC，DE=BF，求证：BE=DF．
11．
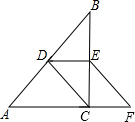如图，在Rt△ABC中，∠ACB=90°，点D、E分别为AB、BC的中点，点F在AC的延长线上，∠FEC=∠B．请问CF=DE成立吗？试说明理由．（提示：直角三角形斜边上的中线等于斜边的一半．）
如图，在Rt△ABC中，∠ACB=90°，点D、E分别为AB、BC的中点，点F在AC的延长线上，∠FEC=∠B．请问CF=DE成立吗？试说明理由．（提示：直角三角形斜边上的中线等于斜边的一半．）
20．计算$\frac{1+\sqrt{2013}（\sqrt{2012}-\sqrt{2011}）}{\sqrt{2011}+\sqrt{2012}+\sqrt{2013}}$+$\sqrt{2011}$=（ ）
| A． | $\sqrt{2010}$ | B． | $\sqrt{2011}$ | C． | $\sqrt{2012}$ | D． | $\sqrt{2013}$ |