题目内容
10．关于x的不等式组$\left\{\begin{array}{l}{x-1＞0}\\{{x}^{3}-{x}^{2}+x≤k}\end{array}\right.$的正整数解只有2和3，则|k-21|+|k-52|+1975的值为（ ）| A． | 2004 | B． | 2005 | C． | 2006 | D． | 2007 |
分析 由不等式组的正整数解只有2和3，得出1＜x≤3，将x=3代入不等式x3-x2+x≤k，可得k≥21，进一步利用绝对值的意义求得答案即可．
解答 解：∵关于x的不等式组$\left\{\begin{array}{l}{x-1＞0}\\{{x}^{3}-{x}^{2}+x≤k}\end{array}\right.$的正整数解只有2和3，
∴不等式的解集为1＜x≤3，
将x=3代入不等式x3-x2+x≤k，得k≥21，
∴|k-21|+|k-52|+1975=k-21+52-k+1975=2006．
故选：C．
点评 此题考查一元一次不等式组的整数解，注意利用特殊值求得k的取值范围是解决问题的关键．
练习册系列答案
相关题目
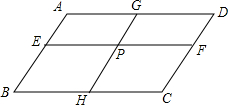如图，在?ABCD中，EF∥AD，GH∥AB，EF，GH相交于点P．
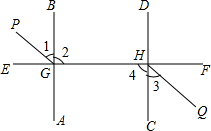如图，AB⊥EF于G，CD⊥EF于H，GP平分∠EGB，HQ平分∠CHF，试找出图中有哪些平行线？并说明理由．