题目内容
12. 如图所示,点A的坐标为(2,1),点B的坐标为(5,3),点C为x轴上一动点,则AC+BC的最小值为5.
如图所示,点A的坐标为(2,1),点B的坐标为(5,3),点C为x轴上一动点,则AC+BC的最小值为5.
分析 过A点作关于x轴的对称点D,连接BD与x轴交于点C,过B作AD的垂线于点E,利用勾股定理得出BD的长.
解答 解:如图,过A点作关于x轴的对称点D,连接BD与x轴交于点C,此时AC+BC=DC+BC=BD,根据两点之间线段最短可知BD的长就是AC+BC的最小值;
过B作AD的垂线于点E,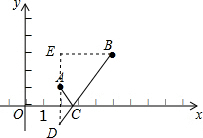
∵点A的坐标为(2,1),点B的坐标为(5,3),
∴BE=5-2=3,DE=1+3=4,
∴利用勾股定理,BD=$\sqrt{D{E}^{2}+B{E}^{2}}$=5
∴AC+BC的最小值为5,
故答案为5.
点评 本题考查了轴对称-最短路线问题,求最小值的方法往往是利用轴对称,找出对称点,然后构造直角三角形,利用勾股定理求线段的长.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
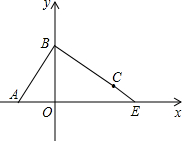 已知A(a,0),B(0,b),a、b满足$\sqrt{a+2}$+b2-8b+16=0,将点A绕点B点逆时针旋转90°,恰好落在点C.
已知A(a,0),B(0,b),a、b满足$\sqrt{a+2}$+b2-8b+16=0,将点A绕点B点逆时针旋转90°,恰好落在点C.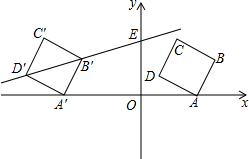 如图,在平面直角坐标系中,四边形ABCD为正方形,A(3,0),D(1,1),点B,C在第一象限内.
如图,在平面直角坐标系中,四边形ABCD为正方形,A(3,0),D(1,1),点B,C在第一象限内.