题目内容
20.计算$\frac{1+\sqrt{2013}(\sqrt{2012}-\sqrt{2011})}{\sqrt{2011}+\sqrt{2012}+\sqrt{2013}}$+$\sqrt{2011}$=( )| A. | $\sqrt{2010}$ | B. | $\sqrt{2011}$ | C. | $\sqrt{2012}$ | D. | $\sqrt{2013}$ |
分析 先通分,合并后把分子部分提$\sqrt{2012}$,然后约分即可.
解答 解:原式=$\frac{1+\sqrt{2013}•\sqrt{2012}-\sqrt{2013}•\sqrt{2011}+\sqrt{2011}•\sqrt{2011}+\sqrt{2011}•\sqrt{2012}+\sqrt{2011}•\sqrt{2013}}{\sqrt{2011}+\sqrt{2012}+\sqrt{2013}}$
=$\frac{2012+\sqrt{2012}•\sqrt{2013}+\sqrt{2011}•\sqrt{2012}}{\sqrt{2011}+\sqrt{2012}+\sqrt{2013}}$
=$\frac{\sqrt{2012}(\sqrt{2011}+\sqrt{2012}+\sqrt{2013})}{\sqrt{2011}+\sqrt{2012}+\sqrt{2013}}$
=$\sqrt{2012}$.
故选C.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
相关题目
5.与算式32+32+32的运算结果相等的是( )
| A. | 33 | B. | 23 | C. | 35 | D. | 36 |
9.下列命题中,是真命题的是( )
| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 相等的角是对顶角 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 在同一平面内,垂直于同一直线的两条直线平行 |
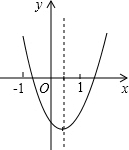 二次函数y=ax2+bx+c的图象如图所示,那么abc,b2-4ac,2a+b,a+b+c四个代数式中,值为正数的有3 个.
二次函数y=ax2+bx+c的图象如图所示,那么abc,b2-4ac,2a+b,a+b+c四个代数式中,值为正数的有3 个.