题目内容
11.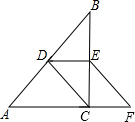 如图,在Rt△ABC中,∠ACB=90°,点D、E分别为AB、BC的中点,点F在AC的延长线上,∠FEC=∠B.请问CF=DE成立吗?试说明理由.(提示:直角三角形斜边上的中线等于斜边的一半.)
如图,在Rt△ABC中,∠ACB=90°,点D、E分别为AB、BC的中点,点F在AC的延长线上,∠FEC=∠B.请问CF=DE成立吗?试说明理由.(提示:直角三角形斜边上的中线等于斜边的一半.)
分析 根据直角三角形斜边上的中线等于斜边的一半可得CD=BD,再根据等边对等角可得∠B=∠DCE,然后求出∠FEC=∠DCE,根据等腰三角形三线合一的性质可得∠CED=90°,然后求出∠CED=∠ECF=90°,再利用“角边角”证明△CDE和△ECF全等,根据全等三角形对应边相等证明即可.
解答 证明:∵∠ACB=90°,点D是AB的中点,
∴CD=BD,
∴∠B=∠DCE,
∵∠FEC=∠B,
∴∠FEC=∠DCE,
∵点E是BC的中点,
∴∠CED=90°,
∴∠CED=∠ECF=90°,
在△CDE和△ECF中,$\left\{\begin{array}{l}{∠CED=∠ECF=90°}\\{CE=EC}\\{∠FEC=∠DCE}\end{array}\right.$,
∴△CDE≌△ECF(ASA),
∴CF=DE.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的性质,全等三角形的判定与性质,熟记各性质并确定出全等三角形是解题的关键.

练习册系列答案
相关题目
9.下列命题中,是真命题的是( )
| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 相等的角是对顶角 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 在同一平面内,垂直于同一直线的两条直线平行 |
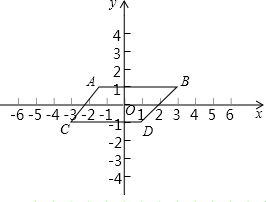 如图所示,平面直角坐标系中有一个平行四边形,点O是平行四边形ABCD对角线的交点,已知点A的坐标为(-1,1),点B的坐标为(3,1).
如图所示,平面直角坐标系中有一个平行四边形,点O是平行四边形ABCD对角线的交点,已知点A的坐标为(-1,1),点B的坐标为(3,1).