题目内容
19.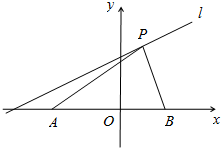 已知A(-5,0),B($\sqrt{5}$,0),P点为直线y=$\frac{1}{3}x+\frac{5}{3}$上的一个动点,P点的横坐标为a,若∠APB为钝角,求a的取值范围.
已知A(-5,0),B($\sqrt{5}$,0),P点为直线y=$\frac{1}{3}x+\frac{5}{3}$上的一个动点,P点的横坐标为a,若∠APB为钝角,求a的取值范围.
分析 根据题意可知点A在一次函数的图象上,然后构造以AB为直径的⊙M,⊙M与直线的交点为P,过点P作PN⊥AB,垂足为N,根据k的意义可知:tan∠PAB=$\frac{1}{3}$,接下来利用锐角三角形函数的定义可求得AN的长度,从而可求得点N的坐标,最后根据当点P在圆内时,∠APB为钝角即可求得a的取值范围.
解答 解:由直线y=$\frac{1}{3}x+\frac{5}{3}$可知:直线与x轴的交点为(-5,0),
∴直线y=$\frac{1}{3}x+\frac{5}{3}$经过A点.
如图所示:构造以AB为直径的⊙M,⊙M与直线的交点为P,过点P作PN⊥AB,垂足为N.
∵AB是⊙M的直径,
∴∠APB=90°.
∴tan∠PAB=$\frac{1}{3}$.
∴cos∠PAB=$\frac{3}{\sqrt{{1}^{2}+{3}^{2}}}$=$\frac{3\sqrt{10}}{10}$.
∴AP=cos∠PAB•AB,AN=cos∠PAB•AP.
∴AN=$\frac{9}{10}$AB=$\frac{9}{10}(\sqrt{5}+5)$=$\frac{9}{2}$+$\frac{9\sqrt{5}}{10}$.
∵ON=AN-OA=$\frac{9}{2}$+$\frac{9\sqrt{5}}{10}$-5=$\frac{9\sqrt{5}}{10}$-$\frac{1}{2}$.
当点P在⊙M内时,∠APB为钝角.
∴当-5<a<$\frac{9\sqrt{5}}{10}$-$\frac{1}{2}$时,∠APB为钝角.
点评 本题主要考查了圆周角定理、锐角三角函数的定义、一次函数的图象和性质,由一次函数的一次项系数k的意义得到tan∠PAB=$\frac{1}{3}$是解题的关键.

| A. | $\left\{\begin{array}{l}x+y=12\\ 2x+y=20\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=12\\ x+2y=20\end{array}\right.$ | C. | $\left\{\begin{array}{l}x+y=20\\ x+2y=12\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=20\\ 2x+y=12\end{array}\right.$ |
 如图,P为矩形ABCD外一点,猜想S△PBC、S△PAC、S△PCD之间的数量关系,并证明.
如图,P为矩形ABCD外一点,猜想S△PBC、S△PAC、S△PCD之间的数量关系,并证明.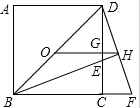 已知:如图,正方形ABCD中,O是BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.
已知:如图,正方形ABCD中,O是BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG. 如图把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′处,∠AE D′=40°,则∠EFB=70°.
如图把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′处,∠AE D′=40°,则∠EFB=70°.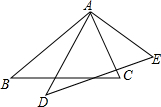 如图,已知△ABC≌△ADE,D是∠BAC的平分线上一点,且∠BAC=70°,则∠CAE=35度.
如图,已知△ABC≌△ADE,D是∠BAC的平分线上一点,且∠BAC=70°,则∠CAE=35度. 已知二次函数y=2x2-4x-6.
已知二次函数y=2x2-4x-6.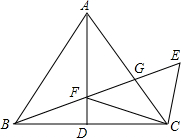 如图,△ABC中,AB=AC,点D为BC边中点,CE∥AB,BE分别交AD、AC于点F、G,连接FC.求证:
如图,△ABC中,AB=AC,点D为BC边中点,CE∥AB,BE分别交AD、AC于点F、G,连接FC.求证: