题目内容
9.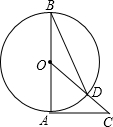 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )| A. | 30° | B. | 22.5° | C. | 20° | D. | 15° |
分析 由AC为圆O的切线,利用切线的性质得到AC与AB垂直,根据∠C的度数求出∠AOC的度数,由OB=OD,利用等边对等角得到∠ABD=∠BDO,利用外角性质即可求出所求角度数.
解答 解:∵AC是圆O的切线,
∴AC⊥AB,
∴∠BAC=90°,
∵∠C=45°,
∴∠AOC=45°,
∵OB=OD,
∴∠ABD=∠ODB=22.5°,
故选B
点评 此题考查了切线的性质,圆周角定理,以及等腰三角形的性质,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
14.根据下面表格中列出来的数据,判断方程ax2+bx=1(a≠0,a,b,c均为常数)的一个解x的取值范围是( )
| x | 3.23 | 3.24 | 3.25 | 3.26 | 3.27 |
| ax2+bx-1 | -0.87 | -0.02 | 0.98 | 1.02 | 1.17 |
| A. | 3.23<x<3.24 | B. | 3.24<x<3.25 | C. | 3.25<x<3.26 | D. | 3.26<x<3.27 |
18.下列计算结果正确的是( )
| A. | (-a3)2=a9 | B. | a6÷a3=a2 | C. | (-$\frac{1}{2}$)-1=-2 | D. | (cos60°-$\frac{1}{2}$)0=1 |
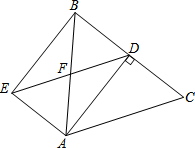 如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.
如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.