题目内容
4.现有无理数$\sqrt{10},\sqrt{11},\sqrt{13}$,其中在$2\sqrt{2}$和$2\sqrt{3}$之间有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 分别求出无理数$\sqrt{10},\sqrt{11},\sqrt{13}$、$2\sqrt{2}$和$2\sqrt{3}$的平方,即可比较大小.
解答 解:$(\sqrt{10})^{2}$=10,$(\sqrt{11})^{2}$=11,$(\sqrt{13})^{2}$=13,$(2\sqrt{2})^{2}$=8,$(2\sqrt{3})^{2}$=12,
∵10,11在8~12之间,
∴$\sqrt{10}$,$\sqrt{11}$在$2\sqrt{2}$和$2\sqrt{3}$之间,
故选:B.
点评 本题考查了估算无理数的大小,解决本题的关键是分别求出无理数$\sqrt{10},\sqrt{11},\sqrt{13}$、$2\sqrt{2}$和$2\sqrt{3}$的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列运算正确的是( )
| A. | a+a=a2 | B. | a2•a3=a6 | C. | (-2a2)2=4a4 | D. | (a-2)2=a2-4 |
9.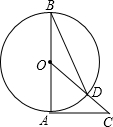 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )
 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )| A. | 30° | B. | 22.5° | C. | 20° | D. | 15° |
 已知网格中每个小正方形的边长是1,在网格中作△ABC,使得AB=$\sqrt{17}$,BC=$\sqrt{13}$,CA=$\sqrt{10}$,并求S△ABC.
已知网格中每个小正方形的边长是1,在网格中作△ABC,使得AB=$\sqrt{17}$,BC=$\sqrt{13}$,CA=$\sqrt{10}$,并求S△ABC. 如图,在△ABC中,AB=4,BC=6,∠B=80°,将△ABC沿射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则∠B′A′C=50°.
如图,在△ABC中,AB=4,BC=6,∠B=80°,将△ABC沿射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则∠B′A′C=50°. 如图,平行四形ABCD中,∠A=100°,则∠B+∠D的度数是160°.
如图,平行四形ABCD中,∠A=100°,则∠B+∠D的度数是160°.