题目内容
1.随着人民生活水平的不断提高,滨州市家庭轿车的拥有量逐年增加,据统计,家景园小区2014年底拥有家庭轿车144辆,2016年底家庭轿车的拥有量达到225辆.(1)若该小区2014年底到2016年底家庭轿车拥有量的年平均增长率都相同,求该小区到2017年底家庭轿车估计将达到多少辆?
(2)为了缓解停车矛盾,该小区决定2017年投资880万元建造若干个停车位,据测算,建造费用分别为室内车位60000元/个,露天车位20000元/个,考虑到实际因素,计划露天车位的数量是室内车位的2倍,那么该小区2017年底车位个数能否满足小区住户的停车需求?
分析 (1)设每年的平均增长率为x,根据2014年底拥有家庭轿车144辆,2016年底家庭轿车的拥有量达到225辆,列出方程进行求解即可;
(2)根据设可建室内车位a个,露天车位b 个,得出b=2a,根据建造费用分别为室内车位60000元/个,露天车位20000元/个,共投资880万元建造,列出方程,进行求解,然后比较即可得出答案.
解答 解:(1)设每年的平均增长率为x,根据题意得:
144(1+x)2=225,
解得:x=$\frac{1}{4}$或x=-$\frac{9}{4}$ (舍去),
则2017年底家庭轿车将达到225×(1+$\frac{1}{4}$)≈281辆.
(2)设可建室内车位a个,露天车位b 个,则b=2a,根据题意得:
60000a+20000b=8800000,
解得a=88,b=176.
则a+b=264<281,不满足需求.
点评 此题考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
9.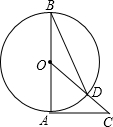 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )
 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )| A. | 30° | B. | 22.5° | C. | 20° | D. | 15° |
 如图,已知直线a∥b,且∠1=60°,则∠2=120°.
如图,已知直线a∥b,且∠1=60°,则∠2=120°. 如图,Rt△ABC中,∠C=90°,AC=4,BC=3,DE是AC边的中垂线,分别交AC,AB于点E,D,则△DBC的周长为( )
如图,Rt△ABC中,∠C=90°,AC=4,BC=3,DE是AC边的中垂线,分别交AC,AB于点E,D,则△DBC的周长为( ) 如图,平行四形ABCD中,∠A=100°,则∠B+∠D的度数是160°.
如图,平行四形ABCD中,∠A=100°,则∠B+∠D的度数是160°. 如图,?ABCD中,延长AD到F,延长CB到E,使BE=DF,连接AE、CF.
如图,?ABCD中,延长AD到F,延长CB到E,使BE=DF,连接AE、CF.