题目内容
19.选择适当的方法解下列一元二次方程:(1)(x-3)2-25=0
(2)x(x+4)=x+4.
分析 (1)将方程(x-3)2-25=0移项得(x-3)2=25,然后再根据直接开平方法求解;
(2)先移项,使方程的右边化为零,然后通过提取公因式x+4对等式的左边进行因式分解.
解答 解:(1)(x-3)2-25=0,
移项得(x-3)2=25,
x-3=±5,
即x-3=5或x-3=-5,
解得x1=8,x2=-2;
(2)移项得x(x+4)-(x+4)=0,
(x-1)(x+4)=0,
x-1=0或x+4=0,
解得x1=1,x2=-4.
点评 本题考查了解一元二次方程-因式分解法,因式分解法解一元二次方程的一般步骤:①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.也考查了用直接开方法求一元二次方程的解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
7.若实数x、y满足$\sqrt{x+y-1}$+(y+3)2=0,则x+y的值为( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
4. 如图所示,图案上各点纵坐标不变,横坐标分别加2,连接各点所得图案与原图案相比( )
如图所示,图案上各点纵坐标不变,横坐标分别加2,连接各点所得图案与原图案相比( )
 如图所示,图案上各点纵坐标不变,横坐标分别加2,连接各点所得图案与原图案相比( )
如图所示,图案上各点纵坐标不变,横坐标分别加2,连接各点所得图案与原图案相比( )| A. | 位置和形状都相同 | B. | 横向拉长为原来的2倍 | ||
| C. | 向左平移2个单位长度 | D. | 向右平移2个单位长度 |
9.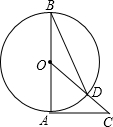 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )
 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD,∠C=45°,则∠ABD的度数是( )| A. | 30° | B. | 22.5° | C. | 20° | D. | 15° |
 如图,已知AD∥BC,∠1=∠2,判断∠BEF与∠DFE的大小关系并说明理由.
如图,已知AD∥BC,∠1=∠2,判断∠BEF与∠DFE的大小关系并说明理由. 已知网格中每个小正方形的边长是1,在网格中作△ABC,使得AB=$\sqrt{17}$,BC=$\sqrt{13}$,CA=$\sqrt{10}$,并求S△ABC.
已知网格中每个小正方形的边长是1,在网格中作△ABC,使得AB=$\sqrt{17}$,BC=$\sqrt{13}$,CA=$\sqrt{10}$,并求S△ABC. 如图,已知直线a∥b,且∠1=60°,则∠2=120°.
如图,已知直线a∥b,且∠1=60°,则∠2=120°.