题目内容
14．根据下面表格中列出来的数据，判断方程ax2+bx=1（a≠0，a，b，c均为常数）的一个解x的取值范围是（ ）| x | 3.23 | 3.24 | 3.25 | 3.26 | 3.27 |
| ax2+bx-1 | -0.87 | -0.02 | 0.98 | 1.02 | 1.17 |
| A． | 3.23＜x＜3.24 | B． | 3.24＜x＜3.25 | C． | 3.25＜x＜3.26 | D． | 3.26＜x＜3.27 |
分析 先对方程ax2+bx=1变形可得ax2+bx-1=0，根据表格可知x的取值范围，从而可以解答本题．
解答 解：∵ax2+bx=1，
∴ax2+bx-1=0，
由表格可知，x=3.24时，ax2+bx-1=-0.02，x=3.25时，ax2+bx-1=0.98，
∴方程ax2+bx=1（a≠0，a，b，c均为常数）的一个解x的取值范围是3.24＜x＜3.25，
故选B．
点评 本题考查估算一元二次方程的近似解，解题的关键是明确题意，找出所求问题需要的条件．
练习册系列答案
相关题目
4．
如图所示，图案上各点纵坐标不变，横坐标分别加2，连接各点所得图案与原图案相比（ ）
如图所示，图案上各点纵坐标不变，横坐标分别加2，连接各点所得图案与原图案相比（ ）| A． | 位置和形状都相同 | B． | 横向拉长为原来的2倍 | ||
| C． | 向左平移2个单位长度 | D． | 向右平移2个单位长度 |
如图，等腰△ABC中，AB=AC，tan∠B=$\frac{3}{4}$，BC=30，D为BC中点，射线DE⊥AC．将△ABC绕点C顺时针旋转（点A的对应点为A′，点B的对应点为B′），射线A′B′分别交射线DA、DE于M、N．当DM=DN时，DM的长为6$\sqrt{10}$+5．
2．下列各式中，合并同类项正确的是（ ）
| A． | -a+3a=2 | B． | x2-2x2=-x | C． | 2x+x=3x | D． | 3a+2b=5ab |
9．
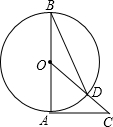如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于点D，连接BD，∠C=45°，则∠ABD的度数是（ ）
如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于点D，连接BD，∠C=45°，则∠ABD的度数是（ ）| A． | 30° | B． | 22.5° | C． | 20° | D． | 15° |
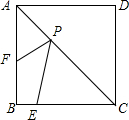如图，正方形ABCD的边长为6，E为BC上的一点，BE=2，F为AB上的一点，AF=3，P为AC上一点，则PF+PE的最小值为$\sqrt{37}$．
如图，Rt△ABC中，∠C=90°，AC=4，BC=3，DE是AC边的中垂线，分别交AC，AB于点E，D，则△DBC的周长为（ ）
4．如果（x-3）（x+5）=x2+ax+b，那么a、b的值是（ ）
| A． | a=8，b=15 | B． | a=-2，b=-15 | C． | a=2，b=-15 | D． | a=-3，b=15 |