题目内容
17.一个三角形,三边长分别为4cm,7cm,xcm,则三角形周长y(cm)与x(cm)的函数关系式是y=x+11,自变量x的取值范围是3<x<11.分析 根据三角形的周长公式,可得函数关系式,根据三角形三边的关系,可得自变量的取值范围.
解答 解:一个三角形,三边长分别为4cm,7cm,xcm,则三角形周长y(cm)与x(cm)的函数关系式是y=x+11,
由三角形的两边之和大于第三边,两边之差小于第三边,得
7-4<x<7+4,即3<x<11,
自变量x的取值范围是 3<x<11,
故答案为:y=x+11,3<x<11.
点评 本题考查了函数关系式,利用三角形的周长公式,利用三角形三边的关系得出自变量的取值范围是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知点A(-3,7)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
| A. | (0,7) | B. | (-1,7) | C. | (-2,7) | D. | (-3,7) |
12.点P(2,-1)向上平移2个单位长度后得到点P′,则点P′的坐标是( )
| A. | (4,-1) | B. | (4,1) | C. | (2,2) | D. | (2,1) |
2. 如图所示,AB⊥BD,AC⊥CD,∠D=35°,则∠A的度数为( )
如图所示,AB⊥BD,AC⊥CD,∠D=35°,则∠A的度数为( )
 如图所示,AB⊥BD,AC⊥CD,∠D=35°,则∠A的度数为( )
如图所示,AB⊥BD,AC⊥CD,∠D=35°,则∠A的度数为( )| A. | 65° | B. | 35° | C. | 55° | D. | 45° |
6.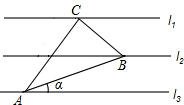 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,△ABC的三个顶点分别在这三条平行直线上,且∠ACB=90°,∠CAB=30°,则tanα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,△ABC的三个顶点分别在这三条平行直线上,且∠ACB=90°,∠CAB=30°,则tanα的值是( )
 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,△ABC的三个顶点分别在这三条平行直线上,且∠ACB=90°,∠CAB=30°,则tanα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,△ABC的三个顶点分别在这三条平行直线上,且∠ACB=90°,∠CAB=30°,则tanα的值是( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{5}$ |
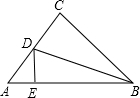 如图,在△ABC中,∠A=50°,∠C=72°,BD是△ABC的角平分线,DE是AB边上的高,∠BDE的度数是61°.
如图,在△ABC中,∠A=50°,∠C=72°,BD是△ABC的角平分线,DE是AB边上的高,∠BDE的度数是61°.