题目内容
5.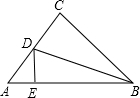 如图,在△ABC中,∠A=50°,∠C=72°,BD是△ABC的角平分线,DE是AB边上的高,∠BDE的度数是61°.
如图,在△ABC中,∠A=50°,∠C=72°,BD是△ABC的角平分线,DE是AB边上的高,∠BDE的度数是61°.
分析 根据三角形的内角和求出∠ABC,由角平行线的性质得到∠DBE=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×58°=29°,在直角三角形中求得∠BDE=90°-29°=61°.
解答 解:∵∠A=50°,∠C=72°,
∴∠ABC=180°-50°-72°=58°,
∵BD是△ABC的角平分线,
∴∠DBE=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×58°=29°,
∵DE⊥AB,
∴∠DEB=90°,
∴∠BDE=90°-29°=61°,
故答案为:61°.
点评 本题考查了三角形的内角和定理,角平分线的性质,直角三角形的性质,熟记定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.夏日来临,玉环杭州大厦服装部试销一款女式防晒服,试销期间对不同颜色的防晒服的销售情况做了统计,如果服装部经理最关心的是哪种颜色的防晒服最畅销,那么对经理最有意义的统计量是( )
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
20.小马虎做了下面四道题,但只做对了一道,他做对的题目是( )
| A. | a7+a6=a13 | B. | a7•a6=a42 | C. | (-8)0=1 | D. | 5-2=-10 |
14. 一个正方体的表面展开图如图所示,则原正方体中字母“A”所在面的对面所标的字是( )
一个正方体的表面展开图如图所示,则原正方体中字母“A”所在面的对面所标的字是( )
 一个正方体的表面展开图如图所示,则原正方体中字母“A”所在面的对面所标的字是( )
一个正方体的表面展开图如图所示,则原正方体中字母“A”所在面的对面所标的字是( )| A. | 玉 | B. | 溪 | C. | 红 | D. | 塔 |
 请你在图中以直线l为对称轴作出所给图形的另一半,并给整个图形一个合适的名称.
请你在图中以直线l为对称轴作出所给图形的另一半,并给整个图形一个合适的名称.