题目内容
3.已知点A(-3,7)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )| A. | (0,7) | B. | (-1,7) | C. | (-2,7) | D. | (-3,7) |
分析 先求出对称轴,再根据二次函数的对称性求解.
解答 解:对称轴为直线x=-$\frac{4}{2×1}$=-2,
设点A关于抛物线对称轴的对称点坐标为(x,7),
则$\frac{-3+x}{2}$=-2,
解得x=-1,
所以,对称点为(-1,7).
故选B.
点评 本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的对称轴,先确定出对称轴解析式是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
18. 如图,直线a、b被直线c所截,下列条件不能保证a、b平行的是( )
如图,直线a、b被直线c所截,下列条件不能保证a、b平行的是( )
 如图,直线a、b被直线c所截,下列条件不能保证a、b平行的是( )
如图,直线a、b被直线c所截,下列条件不能保证a、b平行的是( )| A. | ∠1=∠2 | B. | ∠2=∠3 | C. | ∠3=∠4 | D. | ∠1+∠4=180° |
15.-2的绝对值是( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
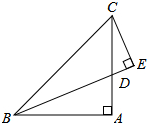 如图,已知,∠BAC=90°,AB=AC,BD是∠ABC的平分线,且CE⊥BD交BD延长线于点E.
如图,已知,∠BAC=90°,AB=AC,BD是∠ABC的平分线,且CE⊥BD交BD延长线于点E.