题目内容

11．计算
（1）$-{2^2}-{（-3）^3}÷{（3.14-π）^0}-{（\frac{1}{20}）^{-1}}$
（2）a3•a3+（2a3）2+（-a2）3．

分析 （1）根据0次幂和负整数指数幂，幂的乘方，即可解答；
（2）根据同底数幂的乘法、积的乘方和幂的乘方，即可解答．

解答 解：（1）原式=-4-（-27）÷（-1）-20  
=-4+27-20                 
=3                      
（2）原式=a6+4a6-a6
=4a6

点评 本题考查了幂的乘方和积的乘方，解决本题的关键是熟记幂的乘方和积的乘方．

练习册系列答案
相关题目
6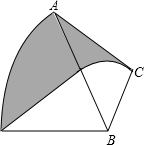．在△ABC中，∠C=90°，∠A=30°，AB=12，将△ABC绕点B按逆时针方向旋转60°，直角边AC扫过的面积等于（　　）
A．24πB．20πC．18πD．6π
2．一个矩形被一条直线分成面积为x，y的两部分，则y与x之间的函数关系用图象表示只可能是（　　）
A．B．C．D．
19．据传说，古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理，在金字塔影子的顶部立一根木杆，借助太阳光线构成两个相似三角形，来测量金字塔的高度．如图所示，木杆EF的长为2m，它的影长FD为3m，测得OA为201m，则金字塔的高度BO为134 m．
6．下列运算正确的是（　　）
A．a2•a3=a6B．a5+a3=a8C．（a3）2=a5D．a5÷a5=1（a≠0）
16．鞋子的“鞋码”和鞋长（cm）存在一种换算关系，下表是几组鞋长和“鞋码”的对应数值（注：“鞋码”是表示鞋子大小的一种号码）．设鞋长为x，“鞋码”为y，试判断点（x，y）在下列哪个函数的图象上（　　）
鞋长（cm）16192123
鞋码（码）22283236
A．y=2x+10B．y=2x-10C．y=-2x+10D．y=-2x-10
3．已知a=3+$\sqrt{2}$，b=3-$\sqrt{2}$，分别求下列代数式的值：
（1）a2-b2
（2）a2-2ab+b2．
20．如图甲，在正方形ABCD的边上有一个动点P以2cm/s的速度，从点B开始B-C-D-A匀速运动，到点A停止．设点P移动时间为t，△ABP的面积为S，S关于t的函数关系如图乙所示，下列结论：①图甲中的BC长是4cm；②图乙中的a的值是8cm2；③当t=l（s），S=3cm2；④当t为0.5s或5.5s时，S=2cm2．其中正确的序号是（　　）
A．①②③B．①②④C．①③④D．②③④
1．要使分式$\frac{x+1}{x-2}$的值为0，则x的值为（　　）
A．x=1B．x=2C．x=-1D．x=-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网