题目内容
6.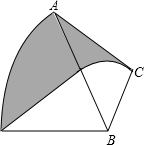 在△ABC中,∠C=90°,∠A=30°,AB=12,将△ABC绕点B按逆时针方向旋转60°,直角边AC扫过的面积等于( )
在△ABC中,∠C=90°,∠A=30°,AB=12,将△ABC绕点B按逆时针方向旋转60°,直角边AC扫过的面积等于( )| A. | 24π | B. | 20π | C. | 18π | D. | 6π |
分析 根据题意可知该阴影部分的面积为两个扇形面积的差,分别计算出两个扇形的面积相减即可得到阴影部分的面积.
解答 解:∵在△ABC中,∠C=90°,∠A=30°,AB=12,
∴BC=$\frac{1}{2}$AB=6,∠ABC=60°,
∴S阴影=$\frac{60•π×A{B}^{2}}{360}$-$\frac{60•π×{BC}^{2}}{360}$=$\frac{60•π×1{2}^{2}}{360}$-$\frac{60•π×{6}^{2}}{360}$=18π.
故选C.
点评 本题考查了扇形的面积的计算,解决此题的关键是根据题目中旋转的角度判断阴影部分的组成.

练习册系列答案
相关题目
16.小晨和小冰两位同学在学习“概率”时做投掷骰子(质地均匀的正方体)实验,他们共做了100次试验,实验结果如下:
(1)计算“2点朝上”的频率和“3点朝上”的频率;
(2)小晨说:“根据实验,一次实验出现4点朝上的概率是$\frac{1}{4}$”;小晨的这一说法正确吗?为什么?
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 10 | 15 | 20 | 25 | 20 | 10 |
(2)小晨说:“根据实验,一次实验出现4点朝上的概率是$\frac{1}{4}$”;小晨的这一说法正确吗?为什么?
11.计算-150+350( )
| A. | 200 | B. | -500 | C. | -200 | D. | 500 |
 如图,直线AB经过原点O,与双曲线y=$\frac{k}{x}(k≠0)$交于A、B两点,AC⊥y轴于点C,且△ABC的面积是8,则k的值是-8.
如图,直线AB经过原点O,与双曲线y=$\frac{k}{x}(k≠0)$交于A、B两点,AC⊥y轴于点C,且△ABC的面积是8,则k的值是-8. 如图,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转,DE,DF分别交线段AC于点M,K.如果MK2+CK2=AM2,则∠CDF的大小是15°(度).
如图,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转,DE,DF分别交线段AC于点M,K.如果MK2+CK2=AM2,则∠CDF的大小是15°(度).