题目内容
若两个相似三角形的面积之比为1：16，则它们的周长之比为（ ）
| A、1：2 | B、1：4 |
| C、1：5 | D、1：16 |
考点：相似三角形的性质
专题：
分析：根据相似三角形面积的比等于相似比的平方求出相似比，再根据相似三角形的周长的比等于相似比解答．
解答：解：∵两个相似三角形的面积之比为1：16，
∴两个相似三角形相似比为1：4，
∴它们的周长之比为1：4．
故选B．
∴两个相似三角形相似比为1：4，
∴它们的周长之比为1：4．
故选B．
点评：本题考查了相似三角形的性质，熟记相似三角形的面积的比、周长的比与相似比的关系是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列运算正确的是（ ）
A、
| ||||
B、（
| ||||
| C、（-a2）3=a6 | ||||
D、a6÷（
|
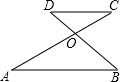已知，如图，AC与BD相交于点O，AB∥CD，如果∠C=30.2°，∠B=50°56′，那么∠BOC为（ ）| A、80°18′ |
| B、50°58′ |
| C、30°10′ |
| D、81°8′ |
解方程
-
=
，去分母所得结论正确的是（ ）
| x+3 |
| 3 |
| x-1 |
| 6 |
| 5-x |
| 2 |
| A、x+3-x+1=15-x |
| B、2x+6-x+1=15-3x |
| C、x+6-x-1=15-x |
| D、x+3-x+1=15-3x |
若分式
的值为0，则x的值是（ ）
| x+3 |
| x |
| A、3 | B、-3 | C、0 | D、±3 |
如图，在平面直角坐标系中，已知四边形ABCD的四个顶点坐标为A（0，6）、B（-3，0）、C（0，-2）、D（4，0），P为AB、DC延长线的交点．下列运算正确的是（ ）
| A、（2a）2=2a2 |
| B、2a+3a=5a |
| C、a2•a3=a6 |
| D、﹙a2﹚3=a5 |