题目内容
4.先观察下面的解题过程,然后解答问题:题目:化简:(2+1)(22+1)(24+1)
解:
(2+1)(22+1)(24+1)
=(2-1)(2+1)(22+1)(24+1)
=(22-1)(22+1)(24+1)
=(24-1)(24+1)
=28-1.
问题:
(1)化简(2+1)(22+1)(24+1)(28+1)…(264+1).
(2)求(3+1)(32+1)(34+1)(38+1)…(3n+1)-$\frac{{9}^{n}}{2}$(n可以写成2n的形式,k为正整数)的值.
分析 (1)仿照例题,式子乘1后结果不变,所以式子乘(2-1),反复运用平方差公式,得出结果;
(2)仿照例题,式子乘1后结果不变,所以式子乘$\frac{1}{2}$(3-1)后,运用平方差公式,计算出结果.
解答 解:(2+1)(22+1)(24+1)(28+1)…(264+1)
=(2-1)(2+1)(22+1)(24+1)(28+1)…(264+1)
=(22-1)(22+1)(24+1)(28+1)…(264+1)
=2128-1;
(2)(3+1)(32+1)(34+1)(38+1)…(3n+1)-$\frac{{9}^{n}}{2}$
=$\frac{1}{2}(3-1)$(3+1)(32+1)(34+1)(38+1)…(3n+1)-$\frac{{9}^{n}}{2}$
=$\frac{1}{2}$(32n-1)-$\frac{{9}^{n}}{2}$
=$\frac{{9}^{n}}{2}-\frac{1}{2}-\frac{{9}^{n}}{2}$
=-$\frac{1}{2}$.
点评 本题主要考查了平方差公式.解决本题的关键是式子乘以(2-1)、$\frac{1}{2}$(3-1)后,运用平方差公式.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
16.如图是一个运算程序,若输出的值为8,则输入值x是( )


| A. | 5 | B. | 8 | C. | 16 | D. | 5或16 |
14.下列说法:①球有1个面;②同一平面内的两点,可以确定一条直线;③两点之间,线段最短;④射线没有端点,其中不正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
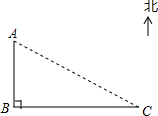 如图,在海上观察所A处.我边防海警发现正南方向60海里的B处有一可疑船只正以每小时20海里的速度向正东方向C处驶去,我边防海警即刻从A处派快艇去拦截.若快艇的速度是每小时$\frac{100}{3}$海里.问快艇最快几小时拦截住可疑船只?
如图,在海上观察所A处.我边防海警发现正南方向60海里的B处有一可疑船只正以每小时20海里的速度向正东方向C处驶去,我边防海警即刻从A处派快艇去拦截.若快艇的速度是每小时$\frac{100}{3}$海里.问快艇最快几小时拦截住可疑船只?