题目内容
13.如果一个自然数从高位到个位是由一个数字或几个数字重复出现组成,那么我们把这样的自然数叫做循环数,重复的一个或几个数字称为“循环节”,我们把“循环节”的数字个数叫做循环节的阶数.例如:525252,它由“52”依次重复出现组成,所以525252是循环数,它是2阶6位循环数,再如:77,是1阶2位循环数,135135135是3阶9位循环数…(1)请你直接写出2个2阶4位循环数,并证明对于任意一个2阶4位循环数,若交换其循环节的数字所得到的新数和原数的差能够被9整除;
(2)已知一个能被9整除的2阶4位循环数,设循环节为ab,求a,b应满足的关系.
分析 (1)根据循环节”的数字个数叫做循环节的阶数,可得答案;
(2)根据一个能被9整除的2阶4位循环数,可得$\frac{2(a+b)}{9}$,根据不等式的性质,可得答案.
解答 解:(1)1717是2阶4位循环数,7171是2阶4位循环数;
证明:设原数为$\overline{abab}$,新数为$\overline{baba}$
即原数1000a+100b+10a+b,新数是1000b+100a+10b+a,
1000b+100a+10b+a-(1000a+100b+10a+b)
=990b-909a
=909(b-a)
=9×101(b-a),
∵a,b为整数,
∴b-a也为整数,
∴新数和原数的差能够被9整除;
(2)该2阶4位循环数为 $\overline{abab}$,
即$\frac{1010a+101b}{9}$
=112a+11b+$\frac{2(a+b)}{9}$,
要使得1010a+101b能被9整除,则需(a+b)能被9整除,
∵0<a≤9,0<b≤9,
∴0<a+b≤18,
∴a,b应满足的关系是a+b=9或a+b=18.
点评 本题考查了因式分解的应用,理解循环阶的阶数是解题关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
3.下列方程中,解为x=2的方程是( )
| A. | x+2=0 | B. | 2+3x=8 | C. | 3x-1=2 | D. | 4-2x=1 |
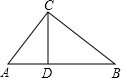 红星中学计划把一块形状如图所示的废弃荒地开辟为生物园,测得AC=75m,BC=100m,AB=125m.如果沿CD修一条水渠且D点在边AB上,水渠的造价为10元/m,问D点在什么位置时,水渠的造价最低?最低造价是多少?
红星中学计划把一块形状如图所示的废弃荒地开辟为生物园,测得AC=75m,BC=100m,AB=125m.如果沿CD修一条水渠且D点在边AB上,水渠的造价为10元/m,问D点在什么位置时,水渠的造价最低?最低造价是多少?
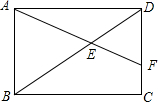 如图,矩形ABCD中,AB=$\sqrt{3}$,BC=$\sqrt{6}$,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于点F.
如图,矩形ABCD中,AB=$\sqrt{3}$,BC=$\sqrt{6}$,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于点F.