题目内容
13．若关于x、y的二元一次方程组$\left\{\begin{array}{l}{x+y=2k+1}\\{x-y=4k-5}\end{array}\right.$的解满足x＜0，y＞0，求k的取值范围．分析 解关于x、y的方程组得x=3k-2、y=-k+3，根据x＜0，y＞0列出关于k的不等式组，解之可得答案．
解答 解：$\left\{\begin{array}{l}{x+y=2k+1}&{①}\\{x-y=4k-5}&{②}\end{array}\right.$，
①+②得，2x=6k-4
∴x=3k-2，
①-②得，2y=-2k+6
∴y=-k+3，
∵x＜0，y＞0
∴$\left\{\begin{array}{l}{3k-2＜0}\\{-k+3＞0}\end{array}\right.$
解得k＜$\frac{2}{3}$．
点评 本题主要考查解二元一次方程组和一元一次不等式组的能力，解题的关键是根据题意列出关于k的不等式组．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
4．
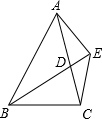如图，已知，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA．下列结论：①△ABD≌△EBC；②∠BCE+∠BCD=180°；③AD=AE=EC；④AC=2CD．其中正确的有（ ） 个．
如图，已知，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA．下列结论：①△ABD≌△EBC；②∠BCE+∠BCD=180°；③AD=AE=EC；④AC=2CD．其中正确的有（ ） 个．| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
5．
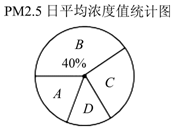环境检测中心在京津冀、长三角、珠三角等城市群以及直辖市和省会城市进行PM2.5[1]检测，某日随机抽取25个监测点的数据，并绘制成统计表和扇形统计图如下：
[1]“PM2.5”是指大气中危害健康的直径小于2.5微米的颗粒物，它造成的雾霾天气对人体健康的危害甚至要比沙尘暴更大．
根据图表中提供的信息解答下列问题：
（1）统计表中的a=5，b=20%，c=24%；
（2）在扇形统计图中，A类所对应的圆心角是72度；
（3）我国PM2.5安全值的标准采用世卫组织（WHO）设定的最宽限值：日平均浓度小于75微克/立方米．请你估计当日环保监测中心在检测100个城市中，PM2.5日平均浓度值符合安全值的城市约有多少个？
环境检测中心在京津冀、长三角、珠三角等城市群以及直辖市和省会城市进行PM2.5[1]检测，某日随机抽取25个监测点的数据，并绘制成统计表和扇形统计图如下：| 类别 | 组别 | PM2.5日平均浓度值 （微克/立方米） | 频数 | 百分比 |
| A | 1 | 15≤浓度值＜30 | 2 | 8% |
| 2 | 30≤浓度值＜45 | 3 | 12% | |
| B | 3 | 45≤浓度值＜60 | a | b |
| 4 | 60≤浓度值＜75 | 5 | 20% | |
| C | 5 | 75≤浓度值＜90 | 6 | c |
| D | 6 | 90≤浓度值＜105 | 4 | 16% |
| 合计 | 25 | 1.00 | ||
根据图表中提供的信息解答下列问题：
（1）统计表中的a=5，b=20%，c=24%；
（2）在扇形统计图中，A类所对应的圆心角是72度；
（3）我国PM2.5安全值的标准采用世卫组织（WHO）设定的最宽限值：日平均浓度小于75微克/立方米．请你估计当日环保监测中心在检测100个城市中，PM2.5日平均浓度值符合安全值的城市约有多少个？
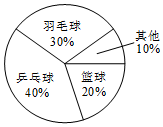某校在“你最喜爱的球类运动”调查中，随机调查了若干名学生（每名学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢篮球的人数比最喜欢乒乓球的人数少8人，则该校被调查的学生总人数为40名．
，那么tanB的值等于（ ）
B. 
C. 
D. 