题目内容
2．
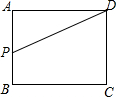如图，矩形ABCD中，AB=3，BC=4，动点P从A点出发，按A→B→C的方向在边AB和BC上移动，若点P的运动路程为x，DP=y，则y关于x的函数图象大致为（ ）| A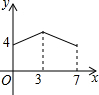． |  | B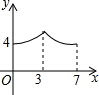． |  | C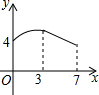． |  | D． |  |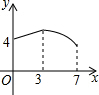
分析 结合图形特点可知点P在A→B路线移动时，DP长在增大，在B→C路线移动时，DP长在减少，通过矩形的边长可以得出xy轴上的值从而确认答案．
解答 解：∵AB=3，BC=4，∠A=90°
∴当动点P在A→B路线移动时，DP2=AP2+AD2=x2+16（0≤x≤3）
∴本段图象应为抛物线，且y随x增大而增大
同理可得动点P在B→C路线移动时，DP2=CP2+DC2=（7-x）2+9（3＜x≤7）
∴本段图象应为抛物线，且y随x增大而减少
故选：B
点评 本题考查了勾股定理、二次函数图象性质，解题的关键是将点P按A→B→C的方向移动时两种情况进行分类讨论．
练习册系列答案
相关题目
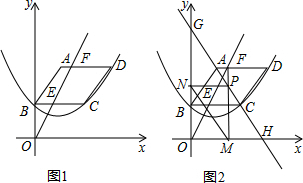
如图，△ABC中，AB=AC，以边BC为直径的⊙O与边AB，AC分别交于D，F两点，过点D作⊙O的切线DE，使DE⊥AC于E．
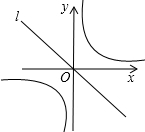如图，已知直线l：y=-x，双曲线y=$\frac{1}{x}$，在l上取一点A（a，-a）（a＞0），过A作x轴的垂线交双曲线于点B，过B作y轴的垂线交l于点C，过C作x轴的垂线交双曲线于点D，过D作y轴的垂线交l于点E，此时E与A重合，并得到一个正方形ABCD，若原点O在正方形ABCD的对角线上且分这条对角线为1：2的两条线段，则a的值为$\sqrt{2}$或$\frac{\sqrt{2}}{2}$．
如图，△ABC中，∠ACB=90°，D为AB上一点，以CD为直径的⊙O交BC于点E，连接AE交CD于点P，交⊙O于点F，连接DF，∠CAE=∠ADF．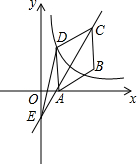
如图，在平行四边形ABCD中，点A、B、C的坐标分别是（1，0）、（3，1）、（3，3），双曲线y=$\frac{k}{x}$（k≠0，x＞0）过点D．