题目内容
11. 如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.
分析 (1)结论:AB是⊙O切线,连接DE,CF,由∠FCD+∠CDF=90°,只要证明∠ADF=∠DCF即可解决问题.
(2)只要证明△PCF∽△PAC,得$\frac{PC}{PA}$=$\frac{PF}{PC}$,设PF=a.则PC=2a,列出方程即可解决问题.
解答 解:(1)AB是⊙O切线.
理由: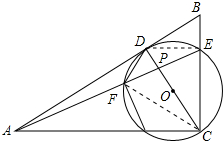 连接DE、CF.
连接DE、CF.
∵CD是直径,
∴∠DEC=∠DFC=90°,
∵∠ACB=90°,
∴∠DEC+∠ACE=180°,
∴DE∥AC,
∴∠DEA=∠EAC=∠DCF,
∵∠DFC=90°,
∴∠FCD+∠CDF=90°,
∵∠ADF=∠EAC=∠DCF,
∴∠ADF+∠CDF=90°,
∴∠ADC=90°,
∴CD⊥AD,
∴AB是⊙O切线.
(2)∵∠CPF=∠CPA,∠PCF=∠PAC,
∴△PCF∽△PAC,
∴$\frac{PC}{PA}$=$\frac{PF}{PC}$,
∴PC2=PF•PA,设PF=a.则PC=2a,
∴4a2=a(a+5),
∴a=$\frac{5}{3}$,
∴PC=2a=$\frac{10}{3}$.
点评 本题考查切线的判定、相似三角形的判定和性质、圆的有关性质等知识,解题的关键是添加辅助线,记住直径所对的圆周角是直角,学会用方程的思想解决问题,属于中考常考题型.

练习册系列答案
相关题目
16.下列各图中,∠1与∠2互为余角的是( )
| A. |  | B. |  | C. |  | D. |  |
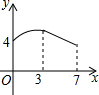
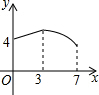
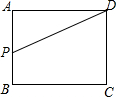 如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在边AB和BC上移动,若点P的运动路程为x,DP=y,则y关于x的函数图象大致为( )
如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在边AB和BC上移动,若点P的运动路程为x,DP=y,则y关于x的函数图象大致为( )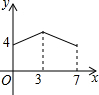
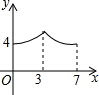
 如图,△ABC中,D、E分别在AB、AC上,DE∥BC,AD:AB=1:3,则△ADE与△ABC的面积之比为1:9.
如图,△ABC中,D、E分别在AB、AC上,DE∥BC,AD:AB=1:3,则△ADE与△ABC的面积之比为1:9.


