题目内容
10.口袋中有12个小球,其中红球x个,黄球(2x+1)个,其余为白球.甲从口袋中任意摸出1个球,若为黄球则甲获胜;然后甲将摸出的球放回口袋中,摇匀,乙从口袋中摸出一个球,若为白球则乙胜.当x为何值时,游戏是公平的?分析 游戏是公平是指甲从口袋中任意摸出1个球是黄球的概率=乙从口袋中摸出一个球为白球的概率,列出方程即可解决.
解答 解;从口袋中任意摸出1个球是黄球的概率为$\frac{2x+1}{12}$,从口袋中摸出一个球为白球的概率为$\frac{11-3x}{12}$,
由题意:$\frac{2x+1}{12}$=$\frac{11-3x}{12}$
解得x=2,
答:x为2时,游戏是公平的.
点评 本题考查游戏公平性,概率等知识,解题的关键是理解题意,学会利用方程解决问题,属于中考常考题型.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
15.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
下列说法正确的是( )
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
| A. | 抛物线的开口向下 | B. | 当x>-3时,y随x的增大而增大 | ||
| C. | 二次函数的最小值是-2 | D. | 抛物线的对称轴是x=-$\frac{5}{2}$ |
 如图,点A是反比例函数图象上y=$\frac{k}{x}$一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为3,则k=-3.
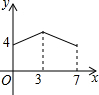
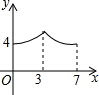
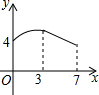
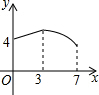
如图,点A是反比例函数图象上y=$\frac{k}{x}$一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为3,则k=-3.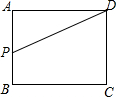 如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在边AB和BC上移动,若点P的运动路程为x,DP=y,则y关于x的函数图象大致为( )
如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在边AB和BC上移动,若点P的运动路程为x,DP=y,则y关于x的函数图象大致为( )