题目内容
7. 如图,△ABC中,AB=AC,以边BC为直径的⊙O与边AB,AC分别交于D,F两点,过点D作⊙O的切线DE,使DE⊥AC于E.
如图,△ABC中,AB=AC,以边BC为直径的⊙O与边AB,AC分别交于D,F两点,过点D作⊙O的切线DE,使DE⊥AC于E.(1)求证:△ABC是等边三角形;
(2)过点E作EH⊥BC,垂足为点H,连接FH,若BC=4,求FH的长.
分析 (1)连接OD.由切线的性质可知OD⊥DE,接下来可证明OD∥AC,由平行线的性质和等腰三角形的性质可证明∠OBD=∠ODB,依据等量代换可得到∠A=∠OBD,于是可证明AC=BC,然后结合已知条件可证明△ABC是等边三角形.
(2)连接BF,作FG⊥BC于点G,连接DC.由直径所对的圆周角是90°证明BF⊥AC,DC⊥AB,由等腰三角形三线合一的性质可得到AD=BD=AF=FC=2,然后再在△FCG中,依据特殊锐角三角函数值可求得FG、CG的长,接下来证明DE∥BF,依据平行线分线段成比例定理可得到AE=EF=1,于是在△EHC中依据特殊锐角三角函数值可求得CE=3,CH=1.5,最后在△HFG中,依据勾股定理可求得HF的长.
解答 解:(1)证明:如图1所示:连接OD.
∵DE是⊙O的切线,
∴OD⊥DE.
∵DE⊥AC,
∴OD∥AC.
∴∠A=∠ODB.
∵OB=OD,
∴∠OBD=∠ODB.
∴∠A=∠OBD.
∴AC=BC.
∵AB=AC,
∴AB=AC=BC.
∴△ABC是等边三角形.
(2)解:连接BF,作FG⊥BC于点G,连接DC.
∵BC是⊙O的直径,
∴∠BFC=90°.
∵△ABC为等边三角形,
∴CF=$\frac{1}{2}$AC=$\frac{1}{2}$BC=2.
同理;BD=AD=2.
∵∠C=60°,∠FGC=90°,
∴FG=$\frac{\sqrt{3}}{2}$FC=$\sqrt{3}$,CG=$\frac{1}{2}$FC=1.
∵DE⊥AC,BF⊥AC,
∴DE∥BF.
∴AE=EF=1.
∴CE=3,CH=1.5.
∴HG=$\frac{1}{2}$.
在Rt△FGH中,由勾股定理可得FH=$\sqrt{F{G}^{2}-G{H}^{2}}$=$\frac{\sqrt{13}}{2}$.
点评 本题主要考查的是切线的性质、圆周角定理、等腰三角形的性质、等边三角形的判定、平行线分线段成比例定理、勾股定理的应用,求得FG和HG的长是解题的关键.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
| A. | 抛物线的开口向下 | B. | 当x>-3时,y随x的增大而增大 | ||
| C. | 二次函数的最小值是-2 | D. | 抛物线的对称轴是x=-$\frac{5}{2}$ |
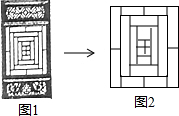 我国传统建筑中,窗框(如图1)的图案玲珑剔透、千变万化,窗框一部分如图2,它是一个轴对称图形,其对称轴有( )
我国传统建筑中,窗框(如图1)的图案玲珑剔透、千变万化,窗框一部分如图2,它是一个轴对称图形,其对称轴有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
| A. |  | B. |  | C. |  | D. |  |
| A. | 1.59×104 | B. | 1.59×105 | C. | 1.59×104 | D. | 15.9×104 |
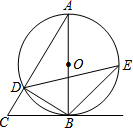 如图,已知△ABC,以AB为直径的⊙O交AC于点D,∠CBD=∠A.
如图,已知△ABC,以AB为直径的⊙O交AC于点D,∠CBD=∠A.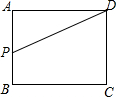 如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在边AB和BC上移动,若点P的运动路程为x,DP=y,则y关于x的函数图象大致为( )
如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在边AB和BC上移动,若点P的运动路程为x,DP=y,则y关于x的函数图象大致为( )