题目内容
(1)分解因式:4x2(y-2)-9(y-2);
(2)解不等式组:
,并把解集在数轴上表示出来.

(2)解不等式组:
|

考点:提公因式法与公式法的综合运用,在数轴上表示不等式的解集,解一元一次不等式组
专题:
分析:(1)首先提取公因式(y-2),进而利用平方差公式分解因式即可;
(2)分别解出不等式,进而在数轴上表示出解集.
(2)分别解出不等式,进而在数轴上表示出解集.
解答: 解:(1)4x2(y-2)-9(y-2)
解:(1)4x2(y-2)-9(y-2)
=(y-2)(4x2-9)
=(y-2)(2x+3)(2x-3);
(2)
,
解①得:x<1,
解②得:x≥-2,
故不等式的解集为:-2≤x<1,
在数轴上表示如图:
 解:(1)4x2(y-2)-9(y-2)
解:(1)4x2(y-2)-9(y-2)=(y-2)(4x2-9)
=(y-2)(2x+3)(2x-3);
(2)
|
解①得:x<1,
解②得:x≥-2,
故不等式的解集为:-2≤x<1,
在数轴上表示如图:
点评:此题主要考查了提取公因式法以及公式法分解因式以及不等式组的解法,熟练掌握公式法分解因式是解题关键.

练习册系列答案
相关题目
 如图,△ABC中,∠ACB=90°,∠A=45°,AC=6,求AB边上的高CD.
如图,△ABC中,∠ACB=90°,∠A=45°,AC=6,求AB边上的高CD.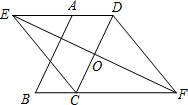 如图,平行四边形ABCD的边CD的垂直平分线与边DA,BC的延长线分别交于点E,F,与边CD交于点O,连结CE,DF.
如图,平行四边形ABCD的边CD的垂直平分线与边DA,BC的延长线分别交于点E,F,与边CD交于点O,连结CE,DF. 小强骑自行车去郊游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象,小强9点离开家,15点回到家,根据这个图象,请你回答下列问题:
小强骑自行车去郊游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象,小强9点离开家,15点回到家,根据这个图象,请你回答下列问题: 已知二次函数y=2x2-4x.
已知二次函数y=2x2-4x. 如图,AB⊥CD,CD⊥BD,∠A=∠FEC.以下是小贝同学证明CD∥EF的推理过程或理由,请你在横线上补充完整其推理过程或理由.
如图,AB⊥CD,CD⊥BD,∠A=∠FEC.以下是小贝同学证明CD∥EF的推理过程或理由,请你在横线上补充完整其推理过程或理由. 如图,△ABC的边BC,AC的垂直平分线相交于点O,连接AO,BO.若∠C=40°,则∠AOB的度数为
如图,△ABC的边BC,AC的垂直平分线相交于点O,连接AO,BO.若∠C=40°,则∠AOB的度数为