Question

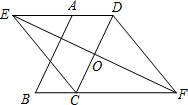如图，平行四边形ABCD的边CD的垂直平分线与边DA，BC的延长线分别交于点E，F，与边CD交于点O，连结CE，DF．
（1）求证：DE=CF；
（2）请判断四边形ECFD的形状，并证明你的结论．

Answer 1

考点：菱形的判定,全等三角形的判定与性质,平行四边形的性质

专题：

分析：（1）通过AAS证得△EOD≌△FOC，故全等三角形的对应边相等：DE=CF；
（2）四边形ECFD是菱形．通过证明DE=EC=CF=DF，得到四边形ABCD是菱形．

解答：（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠EDO=∠FCO，∠DEO=∠CFO，
又∵EF平分CD，
∴DO=CO，
在△EOD与△FOC中，

∠DEO=∠CFO ∠EDO=∠FCO DO=CO

∴△EOD≌△FOC（AAS），
∴DE=CF；

（2）结论：四边形ECFD是菱形．
证明：∵EF是CD的垂直平分线，
∴DE=EC，CF=DF，
又∵DE=CF，
∴DE=EC=CF=DF，
∴四边形ABCD是菱形．

点评：本题考查了全等三角形的判定与性质，菱形的判定以及平行四边形的性质．本题是利用菱形的定义进行证明的．菱形定义：一组邻边相等的平行四边形是菱形（平行四边形+一组邻边相等=菱形）．