题目内容
18．
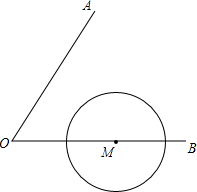如图，∠AOB=60°，M为OB上的一点，OM=5，若以M为圆心，2.5为半径画⊙M，请通过计算说明OA不和⊙M相切．
分析 过M作MN⊥OA于N，解直角三角形求出MN的长，再和半径比较即可．
解答 解：如图，过M作MN⊥OA于N，
则∠ONM=90°，
∵OM=5，∠AOB=60°，
∴MN=OM×sin60°=$\frac{5}{2}$$\sqrt{3}$＞2.5，
∴OA和⊙M外离，
即OA不和⊙M相切．
点评 本题考查了直线和圆的位置关系，解直角三角形的应用，能正确作出辅助线并求出MN的长是解此题的关键，注意：直线和圆有三种位置关系：相离，相交，相切，已知：圆的半径为r，圆心到直线的距离为d，当d＞r时，直线与圆相离，当d=r时，直线与圆相切，当d＜r时，直线与圆相交．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
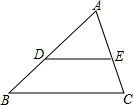如图，在△ABC中，D、E分别在AB、AC上，且$\frac{AD}{AB}$=$\frac{AE}{AC}$，如果AE=3.6cm，EC=2.4cm，AB=9cm．求AD和BD的长．
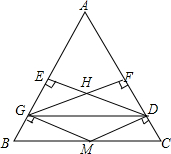已知：如图，在△ABC中，AB=AC，点M在BC上，BM=CM，作MD⊥AC于D，MG⊥AB于G，GF⊥AC于F，DE⊥AB于E，GF、DE交于点H．求证：四边形MDHG为菱形．
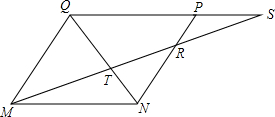如图，已知MNPQ为平行四边形，在QP的延长线上任取-点S，直线MS与NQ交于点T，与NP交于点R．求证：$\frac{1}{MR}+\frac{1}{MS}=\frac{1}{MT}$．