题目内容
在△ABC的三个顶点A(2,-3),B(-4,-5),C(-3,2)中,可能在反比例函数y=
(k>0)的图象上的点是( )
| k |
| x |
| A、点A | B、点B |
| C、点C | D、三个点都在 |
考点:反比例函数图象上点的坐标特征
专题:计算题
分析:先计算三个点的横纵坐标的乘积,再根据反比例函数图象上点的坐标特征可判断若点A在反比例函数y=
(k>0)的图象上,则点C在反比例函数y=
(k>0)的图象上,于是可判断点B在反比例函数图象上.
| k |
| x |
| k |
| x |
解答:解:因为2×(-3)=-6,-4×(-5)=20,-3×2=-6,若点A在反比例函数y=
(k>0)的图象上,则点C在反比例函数y=
(k>0)的图象上,
所以可能在反比例函数y=
(k>0)的图象上的点为B点.
| k |
| x |
| k |
| x |
所以可能在反比例函数y=
| k |
| x |
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
| k |
| x |

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
如图,将半径为2、圆心角为60°的扇形纸片AOB,在直线l上向右作无滑动的滚动至扇形A′O′B′处,则顶点O经过的路线总长为( )


| A、3π | ||
| B、4π | ||
C、
| ||
D、
|
已知点A(-2,y1)、B(-1,y2)、C(2,y3)在二次函数y=2x2+4x-1的图象上,则y1,y2,y3的大小关系是( )
| A、y3>y1>y2 |
| B、y3>y2>y1 |
| C、y1>y3>y2 |
| D、y1>y2>y3 |
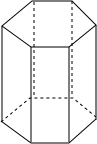 如图,是一个正六棱柱,它的底面边长是3cm,高是6cm.
如图,是一个正六棱柱,它的底面边长是3cm,高是6cm.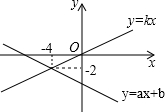 如图,已知一次函数y=ax+b(a≠0)和y=kx(k≠0)的图象交于点P,则一元一次不等式ax+b≤kx的解集是
如图,已知一次函数y=ax+b(a≠0)和y=kx(k≠0)的图象交于点P,则一元一次不等式ax+b≤kx的解集是