题目内容
13.如图1,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,点E在边BC上,AE=BE,点M是AE的中点,联结CM,点G在线段CM上,作∠GDN=∠AEB交边BC于N.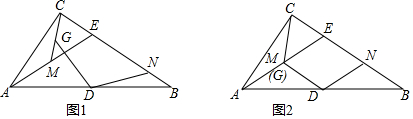
(1)如图2,当点G和点M重合时,求证:四边形DMEN是菱形;
(2)如图1,当点G和点M、C不重合时,求证:DG=DN.
分析 (1)如图2中,首先证明四边形DMEN是平行四边形,再证明ME=MD即可证明.
(2)如图1中,取BE的中点F,连接DM、DF.只要证明△DMG≌△DFN即可.
解答 证明:(1)如图2中,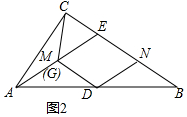
∵AM=ME.AD=DB,
∴DM∥BE,
∴∠GDN+∠DNE=180°,
∵∠GDN=∠AEB,
∴∠AEB+∠DNE=180°,
∴AE∥DN,
∴四边形DMEN是平行四边形,
∵DM=$\frac{1}{2}$BE,EM=$\frac{1}{2}$AE,AE=BE,
∴DM=EM,
∴四边形DMEN是菱形.
(2)如图1中,取BE的中点F,连接DM、DF.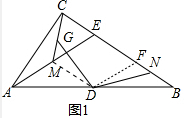
由(1)可知四边形EMDF是菱形,
∴∠AEB=∠MDF,DM=DF,
∴∠GDN=∠AEB,
∴∠MDF=∠GDN,
∴∠MDG=∠FDN,
∵∠DFN=∠AEB=∠MCE,∠GMD=∠EMD+∠CME,、
在Rt△ACE中,∵AM=ME,
∴CM=ME,
∴∠MCE=∠CEM=∠EMD,
∴∠DMG=∠DFN,
∴△DMG≌△DFN,
∴DG=DN.
点评 本题考查菱形的判定和性质、全等三角形的判定和性质、直角三角形斜边中线定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
8.甲,乙,丙,丁四名跳高运动员赛前几次选拔赛成绩如表所示,根据表中的信息,如果要从中,选择一名成绩好又发挥稳定的运动员参加比赛,那么应选甲.
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 185 | 180 | 185 | 180 |
| 方差 | 3.6 | 3.6 | 7.9 | 8.2 |
18.下列式子中一定相等的是( )
| A. | (a-b)2=a2+b2 | B. | a2+b2=(a+b)2 | ||
| C. | (a-b)2=b2-2ab+a2 | D. | (a+b)(a2-ab+b2)=a3-b3 |
 如图,AD是△ABC的中线,点E是AD的中点,若△ABC的面积是16,则△BEC的面积是8.
如图,AD是△ABC的中线,点E是AD的中点,若△ABC的面积是16,则△BEC的面积是8.
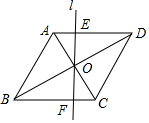 如图,在菱形ABCD中,AB=2,∠ABC=60°,点O为对称中心,过点O的直线l交AD于点E,交BC于点F.
如图,在菱形ABCD中,AB=2,∠ABC=60°,点O为对称中心,过点O的直线l交AD于点E,交BC于点F.