题目内容
3.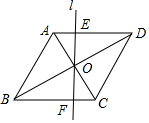 如图,在菱形ABCD中,AB=2,∠ABC=60°,点O为对称中心,过点O的直线l交AD于点E,交BC于点F.
如图,在菱形ABCD中,AB=2,∠ABC=60°,点O为对称中心,过点O的直线l交AD于点E,交BC于点F.(1)求证:△AOE≌△COF;
(2)当∠AOE=30°时,求线段EF的长度.
分析 (1)根据ASA即可判断.
(2)在Rt在Rt△OFC中,∠COF=30°,OF=OCsin60°=$\frac{\sqrt{3}}{2}$,再根据EF=2OF即可解决问题.
解答 解:(1)∵四边形ABCD是菱形,O为对称中心,
∴AD∥BC,AO=OC,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{AO=CO}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AOE≌△COF(ASA).
(2)∵四边形ABCD是菱形,O是对称中心,
∴AB=BC=2,∠ABC=60°,
∴△ABC是等边三角形,
∴AC=2,∠ACB=60°,
∴OC=1,
当∠AOE=30°时,OF⊥BC,
在Rt△OFC中,∠COF=30°,OF=OCsin60°=$\frac{\sqrt{3}}{2}$,
由(1)可知,OE=OF,
∴EF=2OF=$\sqrt{3}$.
点评 本题考查菱形的性质、全等三角形的判定和性质、解直角三角形等知识,解题关键是熟练掌握全等三角形的判定方法,属于中考常考题型.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
18. 如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点0,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )
如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点0,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )
 如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点0,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )
如图,在△ABC中,BD、CE是△ABC的中线,BD与CE相交于点0,点F、G分别是BO、CO的中点,连接AO.若AO=6cm,BC=8cm,则四边形DEFG的周长是( )| A. | 14 cm | B. | 18 cm | C. | 24 cm | D. | 28 cm |
15.下列命题中,真命题是( )
| A. | 两条对角线相等的四边形是矩形 | |
| B. | 两条对角线互相垂直且平分的四边形是正方形 | |
| C. | 等边三角形既是轴对称图形又是中心对称图形 | |
| D. | 有一个角是60°的等腰三角形是等边三角形 |
12.某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如下表:
根据上表中的信息判断,下列结论中错误的是( )
| 成绩(分) | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 人数(人) | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
| A. | 该班一共有40名同学 | |
| B. | 该班学生这次考试成绩的众数是28分 | |
| C. | 该班学生这次考试成绩的中位数是28分 | |
| D. | 该班学生这次考试成绩的平均数是28分 |
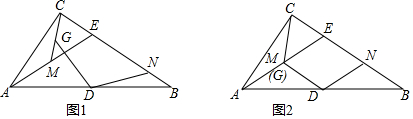
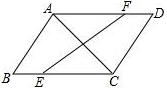 已知:如图,在?ABCD中,点E、F分别在BC、AD上,且AC、EF互相平分,求证:BE=DF.
已知:如图,在?ABCD中,点E、F分别在BC、AD上,且AC、EF互相平分,求证:BE=DF.