题目内容
2.某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计)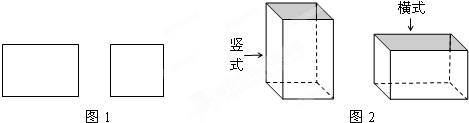
(1)若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;
(2)该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值.
分析 (1)设加工竖式纸盒x个,加工横式纸盒y个,根据两种纸盒每个各需长方形和正方形纸板的张数结合共用正方形纸板1000张、长方形纸板2000张,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设加工竖式纸盒m个,加工横式纸盒n个,根据两种纸盒每个各需长方形和正方形纸板的张数结合共用正方形纸板50张、长方形纸板a张,即可得出关于m、n的二元一次方程组,解之即可用含a的代数式表示出n值,再根据n、a为正整数结合120<a<136即可求出a的值,此题得解.
解答 (1)设加工竖式纸盒x个,加工横式纸盒y个,
根据题意得:$\left\{\begin{array}{l}{x+2y=1000}\\{4x+3y=2000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=200}\\{y=400}\end{array}\right.$.
答:加工竖式纸盒200个,加工横式纸盒400个.
(2)设加工竖式纸盒m个,加工横式纸盒n个,
根据题意得:$\left\{\begin{array}{l}{m+2n=50}\\{4m+3n=a}\end{array}\right.$,
∴n=40-$\frac{a}{5}$.
∵n、a为正整数,
∴a为5的倍数,
又∵120<a<136,
∴满足条件的a为:125,130,135.
点评 本题考查了二元一次方程组的应用以及二元一次方程的应用,解题的关键是:(1)根据两种纸盒每个各需长方形和正方形纸板的张数结合长、正方形纸板的张数列出关于x、y的二元一次方程组;(2)通过解二元一次方程组用含a的代数式表示出n值.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
12.人体内有一种细胞的直径约为0.00000156米,将数0.00000156用科学记数法为( )
| A. | 1.56×10-5 | B. | 1.56×10-6 | C. | 1.56×10-7 | D. | 15.6×10-6 |
12.某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如下表:
根据上表中的信息判断,下列结论中错误的是( )
| 成绩(分) | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 人数(人) | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
| A. | 该班一共有40名同学 | |
| B. | 该班学生这次考试成绩的众数是28分 | |
| C. | 该班学生这次考试成绩的中位数是28分 | |
| D. | 该班学生这次考试成绩的平均数是28分 |
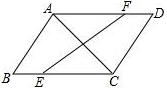 已知:如图,在?ABCD中,点E、F分别在BC、AD上,且AC、EF互相平分,求证:BE=DF.
已知:如图,在?ABCD中,点E、F分别在BC、AD上,且AC、EF互相平分,求证:BE=DF.