题目内容
11.已知一抛物线过点(-3,0)、(-2,-6),且对称轴是x=-1.求该抛物线的解析式.分析 先利用对称性得到抛物线与x轴另一交点是(1,0),则可设交点式y=a(x+3)(x-1),然后把(-2,-6)代入求出a的值即可.
解答 解:∵抛物线的对称轴是直线x=-1,抛物线过点(-3,0)
∴抛物线与x轴另一交点是(1,0),
设抛物线的解析式为y=a(x+3)(x-1),
把(-2,-6)代入得-6=a•(-2+3)•(-2-1),解得a=2,
∴抛物线解析式为y=2(x+3)(x-1),即y=2x2+4x-6.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
2.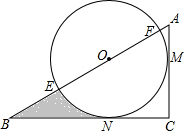 一个含30°角的三角尺与一张圆形硬纸片如图放置在桌面上,圆心O在斜边AB上,三角尺的两直角边与圆相切,切点分别为M、N.若AC=3+$\sqrt{3}$,则阴影部分的面积为( )
一个含30°角的三角尺与一张圆形硬纸片如图放置在桌面上,圆心O在斜边AB上,三角尺的两直角边与圆相切,切点分别为M、N.若AC=3+$\sqrt{3}$,则阴影部分的面积为( )
 一个含30°角的三角尺与一张圆形硬纸片如图放置在桌面上,圆心O在斜边AB上,三角尺的两直角边与圆相切,切点分别为M、N.若AC=3+$\sqrt{3}$,则阴影部分的面积为( )
一个含30°角的三角尺与一张圆形硬纸片如图放置在桌面上,圆心O在斜边AB上,三角尺的两直角边与圆相切,切点分别为M、N.若AC=3+$\sqrt{3}$,则阴影部分的面积为( )| A. | 2$\sqrt{3}$-π | B. | $\sqrt{3}$-$\frac{1}{6}$π | C. | $\sqrt{3}$-$\frac{2}{3}$π | D. | $\frac{9\sqrt{3}}{2}$-$\frac{3}{2}$π |
19. 如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )
如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )
 如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )
如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |

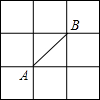 在如图所示的正方形网格中,网线的交点叫做格点.已知A,B是格点,请在图中找格点C,使△ABC是等腰三角形.这样的格点个数有( )
在如图所示的正方形网格中,网线的交点叫做格点.已知A,B是格点,请在图中找格点C,使△ABC是等腰三角形.这样的格点个数有( ) 如图,在平面直角坐标系中,OA=OB=OC=8,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的$\frac{1}{4}$.
如图,在平面直角坐标系中,OA=OB=OC=8,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的$\frac{1}{4}$.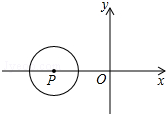 如图所示,在平面直角坐标系xOy中,半径为1的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为2或4.
如图所示,在平面直角坐标系xOy中,半径为1的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为2或4.