题目内容
2.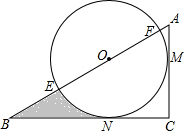 一个含30°角的三角尺与一张圆形硬纸片如图放置在桌面上,圆心O在斜边AB上,三角尺的两直角边与圆相切,切点分别为M、N.若AC=3+$\sqrt{3}$,则阴影部分的面积为( )
一个含30°角的三角尺与一张圆形硬纸片如图放置在桌面上,圆心O在斜边AB上,三角尺的两直角边与圆相切,切点分别为M、N.若AC=3+$\sqrt{3}$,则阴影部分的面积为( )| A. | 2$\sqrt{3}$-π | B. | $\sqrt{3}$-$\frac{1}{6}$π | C. | $\sqrt{3}$-$\frac{2}{3}$π | D. | $\frac{9\sqrt{3}}{2}$-$\frac{3}{2}$π |
分析 本题需先求出直角三角形的边长BC,再利用切线的性质和等腰直角三角形的性质得出四边形ONCM是正方形,然后根据AM=$\sqrt{3}$OM,求得半径,求出直角三角形BON、扇形EON的面积,即可求出阴影部分的面积.
解答 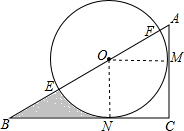 解:∵∠C=90°,∠B=30°,
解:∵∠C=90°,∠B=30°,
∴∠A=60°,
∴BC=$\sqrt{3}$AC=$\sqrt{3}$(3+$\sqrt{3}$)=3+3$\sqrt{3}$,
连接OM、ON,
∵AC,BC与⊙O相切,
∴OM⊥AC,ON⊥BC
∵∠C=90°,OM=ON,
∴四边形ONCM是正方形,
∴OM=ON=NC=CM,
设OM=R,则ON=NC=CM=R,
∴AM=$\frac{\sqrt{3}}{3}$OM=$\frac{\sqrt{3}}{3}$R,
∵CM=AC-AM,
∴R=3+$\sqrt{3}$-$\frac{\sqrt{3}}{3}$R,
解得R=3,
∴CN=3,
∴BN=BC-CN=3+3$\sqrt{3}$-3=3$\sqrt{3}$,
∴S△BON=$\frac{1}{2}$BN•ON=$\frac{1}{2}$×3$\sqrt{3}$×3=$\frac{9\sqrt{3}}{2}$,
∵ON⊥BC,∠B=30°,
∴∠BON=60°,
∴S扇形=$\frac{60π×{3}^{2}}{360}$=$\frac{3π}{2}$,
∴S阴影=S△BON-S扇形=$\frac{9\sqrt{3}}{2}$-$\frac{3}{2}$π.
故选D.
点评 本题主要考查了切线的性质、扇形面积的求法,在解题时要注意面积计算公式和图形的有关性质的综合应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.一个容量为110的样本最大值是152,最小值是50,取组距为10,则可以分为( )
| A. | 9组 | B. | 10组 | C. | 11组 | D. | 12组 |

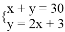
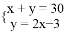
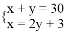
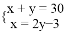
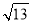 的值在 ( )
的值在 ( )