题目内容
3. 如图,在平面直角坐标系中,OA=OB=OC=8,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的$\frac{1}{4}$.
如图,在平面直角坐标系中,OA=OB=OC=8,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的$\frac{1}{4}$.(1)求点D的坐标;
(2)过点C作CE⊥AD,交AB交于F,垂足为E.求证:OF=OG;
(3)若点F的坐标为($\frac{8}{7}$,0),在第一象限内是否存在点P,使△CFP是以CF为腰长的等腰直角三角形?若存在,请求出点P坐标;若不存在,请说明理由.
分析 (1)过点D作DH⊥AB.利用面积法求得:DH=2,设直线CB的解析式为y=kx+b,将点B、C的坐标代入可求得直线BC的解析式为y=-x+8,将y=2代入得;-x+8=2,解得x=6.从而得到点D的坐标为(6,2);
(2)证明∠AOG=∠CEG,∠GAO=∠OCF,从而可得到Rt△AGO≌Rt△CFO,故此可得到OG=OF;
(3)如图2所示,过点P作PH⊥y轴,垂足为H.依据AAS证明Rt△HPC≌Rt△OFC,于是得到HC=OF=$\frac{8}{7}$,PH=OC=8,从而可求得点P的坐标为(8,9$\frac{1}{7}$);如图3所示:过点P作PH⊥x轴,垂足为H.依据AAS证明Rt△HPF≌Rt△OFC,于是得到OC=FH=8,PH=OF=$\frac{8}{7}$,从而求得点P的坐标为(9$\frac{1}{7}$,$\frac{8}{7}$).
解答 解:(1)如图1,过点D作DH⊥AB.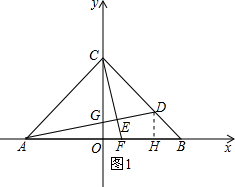
∵$\frac{1}{2}AB•OC=\frac{1}{2}AB•DH$,
∴$\frac{1}{2}×16×8=\frac{1}{2}×16×DH$.
∴DH=2.
设直线CB的解析式为y=kx+b,将点B、C的坐标代入得:$\left\{\begin{array}{l}{b=8}\\{8k+b=0}\end{array}\right.$,
解得:k=-1,b=8.
∴直线BC的解析式为y=-x+8.
将y=2代入得;-x+8=2.
解得x=6.
∴点D的坐标为(6,2).
(2)∵CE⊥AD,CO⊥AO,
∴∠AOG=∠CEG.
又∵∠AGO=∠CGO,
∴∠GAO=∠OCF.
在Rt△AGO和Rt△CFO中,$\left\{\begin{array}{l}{∠AOG=∠COF}\\{AO=CO}\\{∠OAG=∠OCF}\end{array}\right.$,
∴Rt△AGO≌Rt△CFO.
∴OG=OF.
(3)如图2,过点P作PH⊥y轴,垂足为H.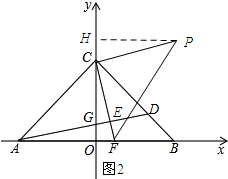
∵△PCF为等腰直角三角形,
∴PC=CF,∠PCF=90°.
∴∠HCP+∠FCO=90°.
又∵∠OCF+∠OFC=90°,
∴∠HCP=∠COF.
在Rt△HPC和Rt△OFC中,$\left\{\begin{array}{l}{∠PHC=∠COF}\\{∠HCP=∠OFC}\\{PC=CF}\end{array}\right.$,
∴Rt△HPC≌Rt△OFC.
∴HC=OF=$\frac{8}{7}$,PH=OC=8.
∴点P的纵坐标=8+$\frac{8}{7}$=$9\frac{1}{7}$.
∴点P的坐标为(8,9$\frac{1}{7}$).
如图3所示:过点P作PH⊥x轴,垂足为H.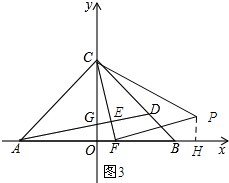
∵△PCF为等腰直角三角形,
∴PC=CF,∠CFP=90°.
∴∠PFH+∠OFC=90°.
又∵∠HFP+∠FPH=90°,
∴∠OHC=∠FPH.
在Rt△HPF和Rt△OFC中,$\left\{\begin{array}{l}{∠OHC=∠FPH}\\{∠PHF=∠FOC}\\{CF=FP}\end{array}\right.$,
∴Rt△HPF≌Rt△OFC.
∴OC=FH=8,PH=OF=$\frac{8}{7}$.
∴点P的横坐标=8+$\frac{8}{7}$=9$\frac{1}{7}$.
∴点P的坐标为(9$\frac{1}{7}$,$\frac{8}{7}$).
点评 本题主要考查的是一次函数的综合应用,解答本题主要应用了全等三角形的性质和判定、等腰直角三角形的性质、待定系数法求一次函数的解析式,掌握本题的辅助线的作法是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 9组 | B. | 10组 | C. | 11组 | D. | 12组 |
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)若9月30日该景区的游客人数为2万人,景区门票原价80元/人,这七天景区门票总收入是多少万元?

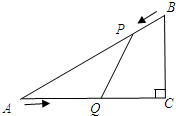 如图,已知在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题:
如图,已知在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题: