题目内容
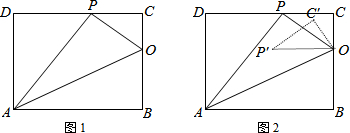
19. 如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )
如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 在Rt△PBN中由PB=2BN可求得∠PBN=60°,由翻折的性质可求得∠QBC=30°,PQ=CQ,在△BQC中由特殊锐角三角函数可求得QC=$\frac{\sqrt{3}}{3}$,从而求得PQ的长.
解答 解:∵M、N分别是AD,BC边上的中点,
∴∠PNB=90°,NB=$\frac{1}{2}$BP.
∴∠PBN=60°.
由翻折的性质可知:∠PBQ=∠CBQ=30°,PQ=CQ.
在Rt△BCQ中,$\frac{QC}{BC}=\frac{\sqrt{3}}{3}$,即$\frac{QC}{1}=\frac{\sqrt{3}}{3}$.
解得:QC=$\frac{\sqrt{3}}{3}$.
∴PQ=$\frac{\sqrt{3}}{3}$.
故选:B.
点评 本题主要考查的是翻折的性质、特殊锐角三角函数值,根据题意求得∠CBQ=30°是解题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
14.一个容量为110的样本最大值是152,最小值是50,取组距为10,则可以分为( )
| A. | 9组 | B. | 10组 | C. | 11组 | D. | 12组 |
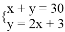
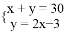
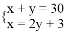
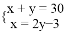
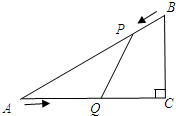 如图,已知在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题:
如图,已知在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题: