题目内容
8.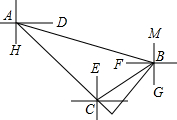 一艘巡逻艇从小岛B出发,沿北偏西75°方向航行10($\sqrt{3}$+1)海里到达A处时,收到由小岛B处求救中心发给它的指令,要求该巡逻艇30分钟内赶到海上C处进行救援,此时C处位于B处南偏西60°,位于巡逻艇南偏东45°,接到指令后巡逻艇立即以每小时50海里的速度赶往C处,问:巡逻艇能否在规定时间内赶到?
一艘巡逻艇从小岛B出发,沿北偏西75°方向航行10($\sqrt{3}$+1)海里到达A处时,收到由小岛B处求救中心发给它的指令,要求该巡逻艇30分钟内赶到海上C处进行救援,此时C处位于B处南偏西60°,位于巡逻艇南偏东45°,接到指令后巡逻艇立即以每小时50海里的速度赶往C处,问:巡逻艇能否在规定时间内赶到?
分析 首先过点C作CN⊥AB于点N,设BN=x海里,由题意可求得∠ACB=105°,∠ABC=45°,∠BAC=30°,然后可得△BCN是等腰直角三角形,BN=CN=x海里,然后在Rt△ACN中,利用三角函数求得AN=$\sqrt{3}$CN=$\sqrt{3}$x海里,继而可得x+$\sqrt{3}$x=10($\sqrt{3}$+1),求得x的值,则可求得答案.
解答 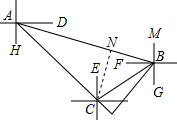 解:巡逻艇能否在规定时间内赶到.
解:巡逻艇能否在规定时间内赶到.
过点C作CN⊥AB于点N,设BN=x海里,
根据题意得:∠ABM=75°,∠CBG=60°,∠CAH=45°,
∵AH∥CE∥MG,
∴∠ACE=∠CAH=45°,∠BCE=∠CBG=60°,
∴∠ACB=∠ACE+∠BCE=105°,
∵∠ABF=90°-∠ABM=15°,∠CBF=90°-∠CBG=30°,
∴∠ABC=45°,
∴∠CAB=180°-∠ACB-∠ABC=30°,
在Rt△BCN中,BN=CN=x海里,
在Rt△ACN中,AN=$\frac{CN}{tan30°}$=$\sqrt{3}$CN=$\sqrt{3}$x(海里),
∵AB=AN+BN=10($\sqrt{3}$+1)海里,
∴x+$\sqrt{3}$x=10($\sqrt{3}$+1),
解得:x=10,
∴AC=2CN=20海里,
∴20÷50=0.4<0.5,
∴巡逻艇能否在规定时间内赶到.
点评 此题考查了方向角问题.注意准确构造直角三角形并解直角三角形是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
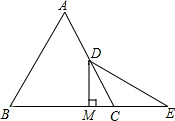 已知,如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD,连接DE,过点D作DM⊥BE于M.
已知,如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD,连接DE,过点D作DM⊥BE于M. 如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为$\frac{2}{3π}$,求图中阴影部分的面积.
如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B、E是半圆弧的三等分点,弧BE的长为$\frac{2}{3π}$,求图中阴影部分的面积.