题目内容
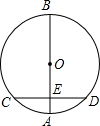
11．
如图，BD是⊙O的直径，弦AC⊥BD，垂足为E，∠AOB=60°，则∠BDC等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 先根据垂径定理由AC⊥BD得到$\widehat{AB}$=$\widehat{BC}$，然后根据圆周角定理求解．
解答 解：∵AC⊥BD，
∴$\widehat{AB}$=$\widehat{BC}$，
∴∠BDC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×60°=30°．
故选A．
点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了垂径定理．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
1．
如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=20，CD=16，那么线段OE的长为（ ）
如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=20，CD=16，那么线段OE的长为（ ）| A． | 10 | B． | 8 | C． | 6 | D． | 4 |
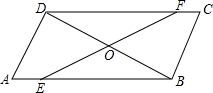如图，?ABCD中，点E、F分别在AB、CD上，且AE=CF，EF与BD相交于点O，求证：OB=OD．
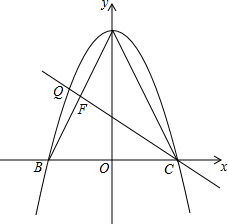如图，在△ABC中，AB=AC，点A（0，4），B（-2，0），C（2，0），F是AB的中点，以A为顶点的抛物线经过B、C两点且与直线CF交于点Q．
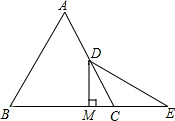已知，如图，△ABC是等边三角形，点D是AC的中点，延长BC到E，使CE=CD，连接DE，过点D作DM⊥BE于M．